Tubular space ship rotates and falls

[Karol]

Homework Statement

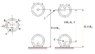
A spaceship has a shape of a hollow tube with outer radius R₁, internal radius R₂ and mass "M". it rotates at angular velocity ω₀. it has 4 short, mass less legs.
In it there is a bar of radius "r" and mass "m". it can be moved instantly to any distance "a" from the center.
The ship starts to fall from height H=10R₂ with the legs up and the inner bar at the center. the computer immediately moves the bar to a certain distance "a" upwards, so when the ship touches the ground the legs are at the bottom. it made half a rotation.
Find a formula for "a" so that the ship will land with legs down.

Homework Equations

Moment of inertia of a cylinder round the center: $I_c=\frac{1}{2}MR^2$
Steiner's theorem: $I_a=I_c+Ma^2$
Free fall: $h=\frac{1}{2}gt^2$
Conservation of angular momentum: $I_c\omega_0=I_1\omega_1$

The Attempt at a Solution

Moment of inertia with the bar at the center:
$$I=\frac{1}{2}\left(R_1^2-R_2^2\right)$$
Moment of inertia with the bar at distance a:
$$I=\frac{1}{2}\left(R_1^2-R_2^2\right)+\frac{1}{2}mr^2+m\left(a+\frac{r}{2}\right)^2$$
$$I=\frac{1}{2}\left[ M\left( R_1^2-R_2^2 \right)+m\left( a^2+ra+\frac{5}{4}r^2 \right)\right]$$
The center of mass when the bar is off the center is at distance C:
$$m\left(a+\frac{r}{2}\right)=C(M+m)\rightarrow C=\frac{\left(a+\frac{r}{2}\right)}{M+m}$$
Free fall between the centers of mass at the top and bottom positions:
$$h=\frac{1}{2}gt^2\rightarrow t^2=\frac{2}{g}\left[10R_2-R_1+\frac{\left(a+\frac{r}{2}\right)}{M+m}\right]$$
The ship makes half a turn, i.e. π[rad]. The new angular velocity:
$$\omega_1=\frac{\pi}{t}=\frac{\pi}{\sqrt{\frac{2}{g}\left[10R_2-R_1+\frac{\left(a+\frac{r}{2}\right)}{M+m}\right]}}$$
Conservation of angular momentum:
$$I_c\omega_0=I_1\omega_1\rightarrow \frac{1}{2}\left(R_1^2-R_2^2\right)\cdot \omega_0=\frac{\frac{1}{2}\left[M\left(R_1^2-R_2^2\right)+m\left(a^2+ra+\frac{5}{4}r^2\right)\right]\pi}{\sqrt{\frac{2}{g}\left[10R_2-R_1+\frac{\left(a+\frac{r}{2}\right)}{M+m}\right]}}$$
It's hard to isolate a, i think i am wrong

 

[rude man]

Since no one has responded in over 12 hrs. I have a comment: in order to rotate the rocket about an axis perpendicular to the spin axis, a torque has to be developed about that perpendicular axis, resulting in a precession motion. But I fail to see how moving the bar provides such a torque.

 

[Karol]

The rocket needn't rotate about an axis perpendicular to the spin axis, it should rotate about an axis parallel to the spin axis, or even the spin axis itself.
I think that moving the bar changes the angular velocity and distance of falling, that's what i made in my calculation.

 

[rude man]

The rocket needn't rotate about an axis perpendicular to the spin axis, it should rotate about an axis parallel to the spin axis, or even the spin axis itself.
I think that moving the bar changes the angular velocity and distance of falling, that's what i made in my calculation.

That doesn't make sense. Rotating about the spin axis will not "right" the rocket.
How do you visualize the bar? Is it coaxial with the spin axis or at rt. angles to that axis?
A drawing would be helpful.

 

[haruspex]

That doesn't make sense. Rotating about the spin axis will not "right" the rocket.
How do you visualize the bar? Is it coaxial with the spin axis or at rt. angles to that axis?
A drawing would be helpful.

There is a diagram at the end of the OP. The rod is parallel to the spin axis, both being horizontal. The idea is to control the rate of spin so that when the tube hits the ground it has done one half rotation. Control is exercised by moving the rod nearer to or further from the spin axis.

 

[haruspex]

$I=\frac{1}{2}\left(R_1^2-R_2^2\right)$

That's not the right formula for an annulus (even if you plug the mass in!). Two solid cylinders of the two radii would have different masses.
Also, the bar has a small MoI even when at the axis of rotation.

$m\left(a+\frac{r}{2}\right)^2$

I think 'a' is supposed to be the distance the rod's centre is displaced.

The center of mass when the bar is off the center is at distance C:

Not sure you are expected to allow for such niceties. If so, you also need to consider that the moment of inertia you just computed is not the one about its mass centre.

 

[rude man]

There is a diagram at the end of the OP. The rod is parallel to the spin axis, both being horizontal. The idea is to control the rate of spin so that when the tube hits the ground it has done one half rotation. Control is exercised by moving the rod nearer to or further from the spin axis.

There is a diagram at the end of the OP. The rod is parallel to the spin axis, both being horizontal. The idea is to control the rate of spin so that when the tube hits the ground it has done one half rotation. Control is exercised by moving the rod nearer to or further from the spin axis.

Yes, I should have looked at the diagram; didn't.

 

[Karol]

Moment of inertia of an annular ring:
$$I=\frac{1}{2}M\left(R_1^2+R_2^2\right)$$
If i take 'a' to be the distance to the center of the rod:
$$I=\frac{1}{2}M\left(R_1^2+R_2^2\right)+\frac{1}{2}mr^2+ma^2$$
The center of mass when the bar is off the center is at distance C:
$$ma=C(M+m)\rightarrow C=\frac{m}{M+m}$$
Free fall between the centers of mass at the top and bottom positions:
$$h=\frac{1}{2}gt^2\rightarrow t^2=\frac{2}{g}\left(10R_2-R_1+\frac{a}{M+m}\right)$$
The ship makes half a turn, i.e. π[rad]. The new angular velocity:
$$\omega_1=\frac{\pi}{t}=\frac{\pi}{\sqrt{\frac{2}{g}\left(10R_2-R_1+\frac{a}{M+m}\right)}}$$
Moment of inertia round the new center of mass:
$$I_1=\frac{1}{2}\left[M\left(R_2^2+R_1^2\right)+mr^2\right]+M\left(\frac{a}{M+m}\right)^2+m\left(a-\frac{a}{M+m}\right)$$
Conservation of angular momentum:
$$I_c\omega_0=I_1\omega_1\rightarrow \frac{1}{2}\left[M\left(R_1^2+R_2^2\right)+mr^2\right]\cdot \omega_0=I_1\omega_1$$
And i have to isolate 'a' from here.

 

[haruspex]

Several places where you have $\frac m{M+m}$ or $\frac a{M+m}$ that should be $\frac {ma}{M+m}$. Check the dimensionalities throughout.

Moment of inertia round the new center of mass:
$I_1=\frac{1}{2}\left[M\left(R_2^2+R_1^2\right)+mr^2\right]+M\left(\frac{a}{M+m}\right)^2+m\left(a-\frac{a}{M+m}\right)$

I don't know how you get those last two terms. They're both dimensionally wrong.
Remember, if you have a moment of inertia about a point other than the mass centre you need to apply the parallel axis theorem in reverse to get it about the mass centre. Anyway, I get:
$I_1=\frac{1}{2}\left[M\left(R_2^2+R_1^2\right)+mr^2\right]+\frac{Mma^2}{M+m}$

 

[Karol]

Thanks, i got the answer
$$I_1=\frac{1}{2}\left[M\left(R_2^2+R_1^2\right)+mr^2\right]+\frac{Mma^2}{M+m}$$
Is that all? i think i finished this problem, right?
Thank you Haruspex

 

[haruspex]

Thanks, i got the answer
$$I_1=\frac{1}{2}\left[M\left(R_2^2+R_1^2\right)+mr^2\right]+\frac{Mma^2}{M+m}$$
Is that all? i think i finished this problem, right?
Thank you Haruspex

Well, you still have the task of isolating a, no?

 

[Karol]

Well i think i will give it up.

 

[rude man]

Well i think i will give it up.

Why? you've done the hard work. Now just invoke conservation of angular momentum, figure out what your ω has to be to right the ship in the time of fall to earth, subtract the initial ω₀ and solve easily for a.
EDIT: sorry, ignore the bit about "..."subtract the initial ω₀ ...".
Just go I(a) = I₀ω₀/ω₁ after you determined ω₁.
Solve for a. Use equation of your post 10 .

 

[Karol]

$$I_c\omega_0=I_1\omega_1\rightarrow \frac{1}{2}\left[M\left(R_1^2+R_2^2\right)+mr^2\right]\cdot \omega_0=I_1\omega_1$$
$$\frac{1}{2}\left[M\left(R_1^2+R_2^2\right)+mr^2\right]\cdot \omega_0=\left\{ \frac{1}{2}\left[M\left(R_2^2+R_1^2\right)+mr^2\right]+\frac{Mma^2}{M+m}\right\} \frac{\pi}{\sqrt{\frac{2}{g}\left(10R_2-R_1+\frac{ma}{M+m}\right)}}$$
$$\sqrt{\frac{2}{g}\left(10R_2-R_1+\frac{ma}{M+m}\right)}=\frac{\pi \left\{ \frac{1}{2}\left[M\left(R_2^2+R_1^2\right)+mr^2\right]+\frac{Mma^2}{M+m}\right\}}{\frac{1}{2}\left[M\left(R_1^2+R_2^2\right)+mr^2\right]\cdot \omega_0}$$
If i raise both sides to square it will be complicated

 

[haruspex]

$$I_c\omega_0=I_1\omega_1\rightarrow \frac{1}{2}\left[M\left(R_1^2+R_2^2\right)+mr^2\right]\cdot \omega_0=I_1\omega_1$$
$$\frac{1}{2}\left[M\left(R_1^2+R_2^2\right)+mr^2\right]\cdot \omega_0=\left\{ \frac{1}{2}\left[M\left(R_2^2+R_1^2\right)+mr^2\right]+\frac{Mma^2}{M+m}\right\} \frac{\pi}{\sqrt{\frac{2}{g}\left(10R_2-R_1+\frac{ma}{M+m}\right)}}$$
$$\sqrt{\frac{2}{g}\left(10R_2-R_1+\frac{ma}{M+m}\right)}=\frac{\pi \left\{ \frac{1}{2}\left[M\left(R_2^2+R_1^2\right)+mr^2\right]+\frac{Mma^2}{M+m}\right\}}{\frac{1}{2}\left[M\left(R_1^2+R_2^2\right)+mr^2\right]\cdot \omega_0}$$
If i raise both sides to square it will be complicated

My suspicion is that you were expected to discard the occurrence of a on the left of that last equation on grounds of its being insignificant, but I don't see any basis for saying that it is. Indeed, it could be more significant than the a on the right.
Arguably "a formula for a" does not have to mean isolating it as "a = ...". The ship's computer should be capable of finding a from the equation you arrived at.

 

[Karol]

Thanks

 

[rude man]

OK this is my last butt-in; talking to myself I know. My apologies to the OP and haruspex. I rejoined only when the OP declared his or her intention to quit. Besides,there's not much else doing on PF right now ...

And so my summary:
$$I_1=\frac{1}{2}\left[M\left(R_2^2+R_1^2\right)+mr^2\right]+\frac{Mma^2}{M+m}$$
or I₁ = I₀ + I(a)
I₁ω₁ = I₀ω₀
(I₀ + I(a))ω₁ = I₀ω₀
π = ω₁T, T = time of descent
10R₂ = (1/2)gT²
Solve for I(a) and thus for a.

 

[haruspex]

OK this is my last butt-in; talking to myself I know. My apologies to the OP and haruspex. I rejoined only when the OP declared his or her intention to quit. Besides,there's not much else doing on PF right now ...

And so my summary:
$$I_1=\frac{1}{2}\left[M\left(R_2^2+R_1^2\right)+mr^2\right]+\frac{Mma^2}{M+m}$$
or I₁ = I₀ + I(a)
I₁ω₁ = I₀ω₀
(I₀ + I(a))ω₁ = I₀ω₀
π = ω₁T, T = time of descent
10R₂ = (1/2)gT²
Solve for I(a) and thus for a.

The snag is that, as Kaspis showed, the time of descent is also a function of a. This is why it appears on the left hand side of K's final equation. As I wrote, I was expecting to be able to argue that this could be ignored, but I see no basis for doing so. Indeed, it may be the dominant effect of a.
It would be eliminated if the question were to state that the rod returned to its original position at the last moment.

 

[rude man]

The snag is that, as Kaspis showed, the time of descent is also a function of a. This is why it appears on the left hand side of K's final equation. As I wrote, I was expecting to be able to argue that this could be ignored, but I see no basis for doing so. Indeed, it may be the dominant effect of a.
It would be eliminated if the question were to state that the rod returned to its original position at the last moment.

I am pretty certain the intent, justifiable or not, was to ignore this complication.
Thanks for answering.
rm