Two marbles colliding elastically on massless strings

[phoebz]

Homework Statement

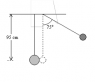
Two marble spheres of masses 30 and 20 grams, respectively, are suspended from the ceiling by massless strings. The lighter sphere is pulled aside, as shown in the diagram, through an angle of 75° and let go. It swings and collides elastically with the other sphere at the bottom of the swing.
a. To what maximum angle will the heavier sphere swing?
b. To what maximum angle will the lighter sphere swing?

-the length of the string is 95cm, see the diagram attached

Homework Equations

M=30g, V= speed of M, θ1 =angle of M
m=20g, v= speed of m, θ2 =angle of m

Law of conservation of kinetic energy:
1/2mv^2 + 1/2MV^2 = 1/2mv'^2 + 1/2MV'^2

Law of conservation of momentum:
x component: mv(cos75) =mv'(cosθ2) + MV'(cosθ1)
y component: mv(sin75) =mv'(sinθ2) + MV'(sinθ1)

The Attempt at a Solution

First I tried to find the velocity of m after it was released with the equation:
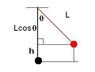
v =sqrt(2gLsinθ)
and got 4.24m/s

Then I plugged that into the law of conservation of KE and got:
1/2(20g)(4.24^2) = 1/2(20g)v^2 + 1/2(30)V^2
179.776 = 10v^2 + 15V^2

Then I plugged in the variables for the momentum equations:
x component: 20(4.24)(cos75) =20v'(cosθ2) + 30V'(cosθ1)
y component: 20(4.24)(sin75) =20v'(sinθ2) + 30V'(sinθ1)

I have tried all sorts of algebra to solve for the unknowns but keep getting complex equations that seem useless. Any help would be greatly appreciated!

 

[azizlwl]

For conservation of momentum, the values should be calculated just after the collision, θ=0.

 

[NoPoke]

After release the potential energy in the initial position is being converted into kinetic energy. The two balls then collide and the kinetic energy is shared.

How is the KE and PE related? Are there any points where the relationship between KE and PE is easy to solve?

 

[phoebz]

For conservation of momentum, the values should be calculated just after the collision, θ=0.

So if I was to use my momentum equations from before in this way I would get

x component: 20(v)(cos75) =20v'(cos0) + 30V'(cos0)
20(v)(cos75) =20v' + 30V'

y component: 20(v)(sin75) =20v'(sin0) + 30V'(sin0)
20(v)(sin75) = 0 ?

I am a little confused. Do I use the initial velocity of the smaller mass (4.24m/s?) to figure out momentum before the collision? Or do I use the above equations to calculate the marbles momentum after the collision and ignore the initial velocity of the smaller marble?

 

[phoebz]

After release the potential energy in the initial position is being converted into kinetic energy. The two balls then collide and the kinetic energy is shared.

How is the KE and PE related? Are there any points where the relationship between KE and PE is easy to solve?

KE and PE are related through the equation PE = KE, mgh=1/2mv^2 (is that right in this case?). That is what I used to find the initial velocity of the 20g marble. But I am not sure if I needed to do that? I am also unsure of how else I could use the equation mgh=1/2mv^2.

 

[NoPoke]

PE+KE = total energy = constant as there is no friction or other loss mechanism to consider.

Where is PE highest? Where is PE lowest? Same questions for KE

 

[phoebz]

But how will I be able to find angles from this?

 

[Doc Al]

Try this. How fast is the lighter marble moving just before it hits the heavier marble? Then use the conservation laws to find their speeds immediately after the collision.

 

[phoebz]

To Doc Al:
I have figured out the velocity of the 20g marble is 3.715m/s just as it is about to hit the 30g marble using h= L- sqrt(L^2-x^2) and PE=KE.

I know that I have to use the law of conservation of KE and momentum to figure out the rest, but, I do not know when I should be breaking things into x and y components of momentum.
I have been trying to use these formulas:

x: mvcos(75)= mv'cosθ + MV'cosθ
y: mvsin(75) = mv'sinθ + MV'sinθ

KE law: 10v^2 = 10v'^2 + 15V^2
where v = 3.715m/s
Should I have broken this question into x and y components like this?

 

[Doc Al]

I know that I have to use the law of conservation of KE and momentum to figure out the rest, but, I do not know when I should be breaking things into x and y components of momentum.

At the point of collision, the marbles are moving horizontally. No need for anything but a single direction.

I have been trying to use these formulas:

x: mvcos(75)= mv'cosθ + MV'cosθ
y: mvsin(75) = mv'sinθ + MV'sinθ

KE law: 10v^2 = 10v'^2 + 15V^2
where v = 3.715m/s
Should I have broken this question into x and y components like this?

No. The 75° angle was the initial position of the marble. It has nothing to do with the collision.

 

[phoebz]

Okay, thanks!

So this is what I came up with:

v= 3.715m/s (From my previous post) m=20g
V=0 M=30g

momentum:
mv=MV' + mv'
20g(3.715m/s) = 30gV' + 20gv'
74.3 = 30V' +20v'

KE:
1/2mv^2 = 1/2mv'^2 +1/2MV'^2
10(3.715)^2 = 10v'^2 + 15V'^2 (sqrt root both sides)
37.15 = 10v' + 15V'
v' = (37.15 - 15V')/10

But whenever I substitue v' into the momentum equation (those parts are in red). everything cancels out and I get v' = v'...

 

[TSny]

10(3.715)^2 = 10v'^2 + 15V'^2 (sqrt root both sides)
37.15 = 10v' + 15V'

Check that step.

 

[phoebz]

Ok, I have changed that to:

10(3.715)^2 = 10v'^2 +15V'^2

sqrt(138) = sqrt(10) v'^2 + sqrt(15) V'^2

And when I solved for V' I got -0.000159? I think I messed up again,
I apologize for my rusty algebra skills...

 

[phoebz]

Do I have the right steps though? Or are my steps and math wrong?

(thank you for all your help so far!)

 

[TSny]

Ok, I have changed that to:

10(3.715)^2 = 10v'^2 +15V'^2

sqrt(138) = sqrt(10) v'^2 + sqrt(15) V'^2

And when I solved for V' I got -0.000159? I think I messed up again,
I apologize for my rusty algebra skills...

It looks like the algebra is giving you a little bit of difficulty. When you take the square root of the right hand side of the equation you should actually get
$\sqrt{10v'^{2}+15V'^{2}}$

This cannot be simplified. In particular $\sqrt{a+b}$$\neq$$\sqrt{a}$+$\sqrt{b}$. So, taking the square root of both sides does not help.

A good approach is to go back to your momentum equation 74.3 = 30V' +20v' and solve it for v' in terms of V'.
Then substitute this expression for v' into the energy equation 10(3.715)² = 10v'² +15V'². It's a bit messy, but you should then be able to solve for V'.

 

[phoebz]

Awesome! I finally got values for the velocities. V'= 2.972m/s, v'=-0.743m/s.

So this means the large marble moves forwards with ~3m/s and the small marble goes back the way it came with ~1m/s?

Then I can find the heights of each marble after the collision:
small: 1/2mv^2 =mgh +1/2mv'^2
10(3.715)^2 = 20g(9.80)h + 10(0.743m/s)^2
h= 0.676m

large: 1/2mv^2 =mgh
15(2.972)^2 = 30g(9.8)h
h=0.451m

Can I then use the formula h= sqrt(0.95^2 -x^2) to find the horizontal distances the marbles travel (see the diagram again). and then use the length of the string and x to find the angle?

Ok, I attached a diagram showing how I used x and L to find theta for each marble. Is this logical?

Thanks for takin the time :)

 

[NoPoke]

redraw the diagram of the final positions with all the heights that you know and all the lengths that you know.

Does it look simpler now?

Hint try to make a 1/10th scale drawing , don't forget to use a compass.

 

[NoPoke]

Pheobz, I can see you have added a triangle and want to calculate a horizontal displacement. But do you need that horizontal displacement, since its not part of the answer you have to give?What lengths do you know? What heights do you know? What do you know about the shape of the paths of the two marbles? where are your heights measured from?

If you don't have a compass use a bit of string tied around a pencil. If the algebra/ trigonometry is unclear then often the best way to see a way forward is to make a drawing. Geometry really can help you here.

 

[TSny]

Awesome! I finally got values for the velocities. V'= 2.972m/s, v'=-0.743m/s.

That looks right!

So this means the large marble moves forwards with ~3m/s and the small marble goes back the way it came with ~1m/s?

Yes.

Then I can find the heights of each marble after the collision:
small: 1/2mv^2 =mgh +1/2mv'^2
10(3.715)^2 = 20g(9.80)h + 10(0.743m/s)^2
h= 0.676m

No. Here you want to think about a new problem where the small mass starts at the lowest point with a velocity of -0.743 m/s and swings up to it's max height h. In fact, you want to do the same calculation that you did below for the large mass.

large: 1/2mv^2 =mgh
15(2.972)^2 = 30g(9.8)h
h=0.451m

Yes, this is how you should have also done the small mass.

[Note added: Strictly speaking, you should be converting grams to kg if you're working in the SI system of units. However, since the mass occurs in each term of your equations, you can get by without converting.]

 

[phoebz]

Pheobz, I can see you have added a triangle and want to calculate a horizontal displacement. But do you need that horizontal displacement, since its not part of the answer you have to give?

I found the horizontal displacement so that I could find the angle theta, I found 'x' using the formula h= L- sqrt(L^2-x^2). Then I went sin(theta) =x/L to find the angle for each marble, does this work?

And thank you TSny, I think I have the right value for the small marble now, 0.028m!

 

[NoPoke]

what is the relationship between

string length x cosine(theta)
and h

?

 

[phoebz]

They add together to make the adjacent side of the angle?

I tried going cos(theta) = [L cos(theta) +h] /L

but the Lcos(theta)s both cancel out :s

 

[NoPoke]

There is something wrong with your equation..

what does L cos(theta) + h add up to?

 

[phoebz]

The the length of the string? I am really not sure :s, I thought I had it figured

 

[Doc Al]

The the length of the string?

Right.

When comparing the raised position to the bottom position, the length of the string is of course the same. What differs is the height. What's the vertical distance below the pivot point (the ceiling) in each case? Use that to figure out the height h.

 

[phoebz]

Awesome! I finally think I have it! Thank you everyone :D