benca
- 19
- 0
- Homework Statement
- A two-point source operates at a frequency of 1.0 Hz to produce an interference pattern in a ripple tank. The sources are 2.5 cm apart and the wavelength of the waves is 1.2 cm.
Calculate the angles at which the nodal lines in the pattern are located far from the sources. (Assume the angles are measured from the central line of the pattern.)
- Relevant Equations
- λ = (xn/L)[d/(n - 0.5)]
dsinθn= (n - 0.5)λ
xn = perpendicular distance from the right bisector t o the point Pn on the nodal line
L = distance from midpoint between the two sources to the point Pn
n = number of the nodal line
d= separation of the sources
I'm having trouble understanding what it's asking me. "Calculate the angles at which the nodal lines in the pattern are located far from the sources." I assume they are very far away, making lines PnS1 and PnC parallel. Is the question asking me to calculate θ' in the example?
"nodal lines" should I solve for several different values of n? I was thinking of using dsinθn= (n - 0.5)λ to solve for θn since θn = θ' If that's right, for how many nodal lines do I do this? Also why would they provide the frequency? Attached in a diagram from a previous example.
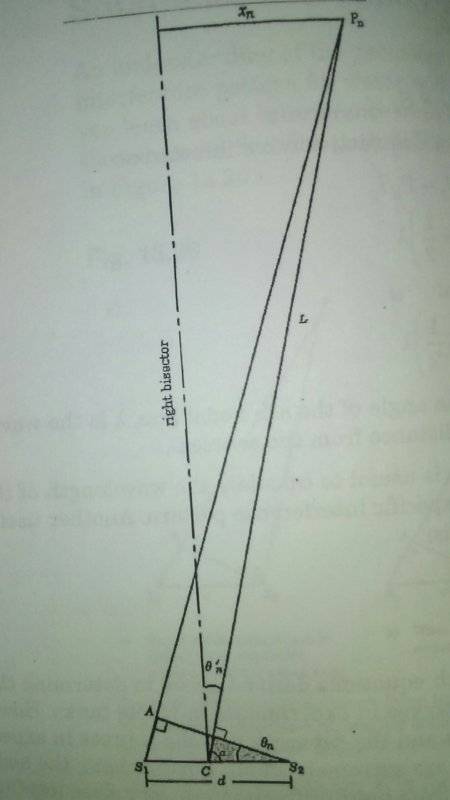
"nodal lines" should I solve for several different values of n? I was thinking of using dsinθn= (n - 0.5)λ to solve for θn since θn = θ' If that's right, for how many nodal lines do I do this? Also why would they provide the frequency? Attached in a diagram from a previous example.