- 19,851
- 10,883
Definition/Summary
A Gaussian beam is an electromagnetic wave, usually a laser beam, with a Gaussian cross-sectional irradiance pattern. The Gaussian irradiance profile results in minimal spreading due to diffraction effects.
The spot size w represents the radius or half-width at which the irradiance is a factor of 1/e^2 less than the central-axis irradiance.
Equations
For a Gaussian laser beam propagating along the z-axis, the electric field strength is a Gaussian function of the transverse (or radial) coordinate r:
E = E_0 \cdot e^{-r^2/w^2}
where Eo and w are both functions of z.
It is common practice to work in terms of the irradiance, which is proportional to the square of the electric field, so that
I = I_0(z) \cdot e^{- 2 r^2 / w(z)^2}The various parameters of a Gaussian beam are related as follows:
\begin{align*}<br /> <br /> \theta & = & & \frac{\lambda}{\pi \ w_o} <br /> & = & & \sqrt{\frac{\lambda}{\pi \ z_R}} \<br /> & = & & \ \frac{w_o}{z_R}<br /> \\ \\<br /> <br /> w_o & = & & \frac{\lambda}{\pi \ \theta} <br /> & = & & \sqrt{\frac{\lambda \ z_R}{\pi}} \\ \\<br /> <br /> z_R & = & & \frac{\pi \ w_o^2}{\lambda} <br /> & = & & \frac{\lambda}{\pi \ \theta^2} \\ \\ <br /> <br /> b & = & & 2 \ z_R \\<br /> <br /> \end{align*}Moreover,
\begin{align*}<br /> <br /> w(z) & = & & w_o \sqrt{1 + \left(\frac{z}{z_R}\right)^2} \\ \\<br /> <br /> R(z) & = & & z + z_R^2/z <br /> \ = \ z \left[ 1 + \left( \frac{z_R}{z} \right) ^2 \right]<br /> <br /> \end{align*}
Extended explanation
Definitions of terms
(SI units for quantities are shown in parantheses)
* This entry is from our old Library feature, and was originally created by Redbelly98.
A Gaussian beam is an electromagnetic wave, usually a laser beam, with a Gaussian cross-sectional irradiance pattern. The Gaussian irradiance profile results in minimal spreading due to diffraction effects.
The spot size w represents the radius or half-width at which the irradiance is a factor of 1/e^2 less than the central-axis irradiance.
Equations
For a Gaussian laser beam propagating along the z-axis, the electric field strength is a Gaussian function of the transverse (or radial) coordinate r:
E = E_0 \cdot e^{-r^2/w^2}
where Eo and w are both functions of z.
It is common practice to work in terms of the irradiance, which is proportional to the square of the electric field, so that
I = I_0(z) \cdot e^{- 2 r^2 / w(z)^2}The various parameters of a Gaussian beam are related as follows:
\begin{align*}<br /> <br /> \theta & = & & \frac{\lambda}{\pi \ w_o} <br /> & = & & \sqrt{\frac{\lambda}{\pi \ z_R}} \<br /> & = & & \ \frac{w_o}{z_R}<br /> \\ \\<br /> <br /> w_o & = & & \frac{\lambda}{\pi \ \theta} <br /> & = & & \sqrt{\frac{\lambda \ z_R}{\pi}} \\ \\<br /> <br /> z_R & = & & \frac{\pi \ w_o^2}{\lambda} <br /> & = & & \frac{\lambda}{\pi \ \theta^2} \\ \\ <br /> <br /> b & = & & 2 \ z_R \\<br /> <br /> \end{align*}Moreover,
\begin{align*}<br /> <br /> w(z) & = & & w_o \sqrt{1 + \left(\frac{z}{z_R}\right)^2} \\ \\<br /> <br /> R(z) & = & & z + z_R^2/z <br /> \ = \ z \left[ 1 + \left( \frac{z_R}{z} \right) ^2 \right]<br /> <br /> \end{align*}
Extended explanation
Definitions of terms
(SI units for quantities are shown in parantheses)
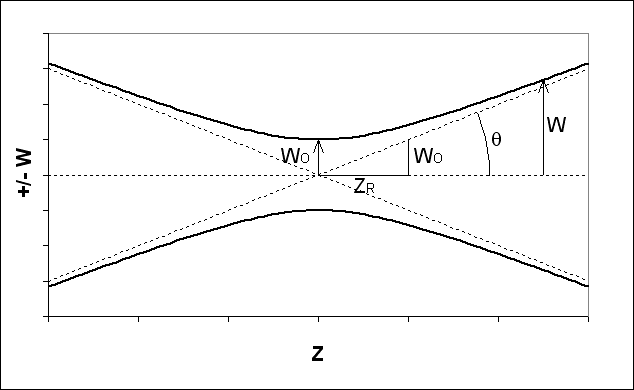
b = confocal parameter (m)
E = electric field (V/m)
Eo = E at r=0
I, Io = irradiance (W/m2)
r = transverse or radial coordinate (m)
R(z) = radius of curvature of wavefronts (m)
w(z) = spot size (m)
wo = beam waist (m), or spot size at z=0
z = longitudinal coordinate (m)
zR = Rayleigh range
λ = wavelength (m)
θ = divergence half-angle
Descriptive figureE = electric field (V/m)
Eo = E at r=0
I, Io = irradiance (W/m2)
r = transverse or radial coordinate (m)
R(z) = radius of curvature of wavefronts (m)
w(z) = spot size (m)
wo = beam waist (m), or spot size at z=0
z = longitudinal coordinate (m)
zR = Rayleigh range
λ = wavelength (m)
θ = divergence half-angle
* This entry is from our old Library feature, and was originally created by Redbelly98.
Last edited by a moderator: