Understanding Pressure and Volume in a U-shaped Tube

[Waffle24]

Homework Statement

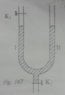
The open legs 1 and 2 of an U-shaped tube have a diameter of 2 cm^2. In leg 2, mercury is poured. When the distance is 16cm from the mercury level up to the valve K1 , then the valve gets closed. The barometer reading is 76cm Hg.

a) How big is the pressure of the sealed air?
b) Opening valve K2, then the mercury in leg 2 appears to drop faster than leg 1. Explain this.
c) When the sealed air has reached a length of 19 cm, this valve K2 is closed.
How big is the pressure of the sealed air and how much cm^3 Hg has been drained?

So I had no trouble answering question a, the answer is air pressure = sealed air.

Now comes question b. My teacher told me that the pressure in leg 1 is bigger than the pressure in leg 2, that's why the mercury in leg 2 is dropping faster, but I still fail to see how the pressure is of leg 1 is bigger than leg 2.

c) I'm kinda lost on what equation(s) I have to use to calculate the pressure and how much cm^3 Hg has been drained. It's like a few informations are missing, but then again I might be wrong and there is way out there to calculate it.

Homework Equations

So far I've got only :
- P = F/A (P = Pressure, F = Force, A = Area)

- P1 x v1 = P2 x v2 ( P= Pressure , v = Volume)

The Attempt at a Solution

N/A

 

[mjc123]

What happens to the pressure of the air in leg 1 when the mercury level drops? What about leg 2?

 

[Waffle24]

Well the pressure of the air in leg 1 is equal to the air pressure if both K1 and K2 are closed, so if you open up K2 the air pressure in leg 1 will be less than the air pressure in leg 2, and so will the liquid drop faster in leg 2, because the air pressure in leg 2 is bigger than the air pressure of leg 1. I guess the closed air pressure in leg 1 depends on the outside air pressure.

 

[mjc123]

OK. Now if the air trapped in leg 1 was originally a column 16 cm long, now it is 19 cm long, what is the pressure of this trapped air?
What is the difference in the air pressures in legs 1 and 2?
What is the difference in height of the mercury columns in legs 1 and 2?
So how much mercury has been drained?

 

[Waffle24]

OK. Now if the air trapped in leg 1 was originally a column 16 cm long, now it is 19 cm long, what is the pressure of this trapped air?

I'm stuck at here, like is there an equation to calculate the new pressure(trapped air)?

On edit : I think I've figured it out already, since both length and the area of both column are known, we can calculate the Volume and then apply Boyle’s Law.

 

[Waffle24]

Sorry for the late reply.

V = 2 x 16 = 32 cm
V = 2 x 19 = 38 cm

P1 x V1 = P2 x P2

76 x 32 = P2 × 38
2432 = 38P2
P2 = 64 cmHg
Trapped air pressure = 64cmHg

Air pressure Difference between leg 1 and 2 :
76 - 64 = 12 cmHg

What is the difference in height of the mercury columns in legs 1 and 2?
19 cmHg - 16 cmHg = 3 cmHg

Am I right? Though why do you need the difference in air pressure and difference in height?

If I am correct you need to calculate the volume of how much mercury has been drained right?
So wouldn't it be :
V = A × h
V = 2 × 19
V = 38 cm^3

I guess I'm missing something. D:

 

[mjc123]

What is the difference in height of the mercury columns in legs 1 and 2?
19 cmHg - 16 cmHg = 3 cmHg

Do you think the mercury in leg 2 hasn't moved? Why? What about your answer to part b?
Now the pressure above the mercury in leg 2 is atmospheric. The pressure above the mercury in leg 1 is 64 cm Hg. At what distance below the mercury surface in leg 1 will the pressure be equal to atmospheric? The mercury level in leg 2 will be at this height. Can you see why?

 

[Waffle24]

Do you think the mercury in leg 2 hasn't moved? Why? What about your answer to part b?

Well it has moved, because the air pressure was higher than the trapped air.

At what distance below the mercury surface in leg 1 will the pressure be equal to atmospheric?

12cmHg

What is the difference in height of the mercury columns in legs 1 and 2?

So it will be :
19cmHg - 12 cmHg = 7 cmHg

 

[mjc123]

So it will be :
19cmHg - 12 cmHg = 7 cmHg

Why do you say that? Can you draw a diagram of what you think the system looks like at this stage?

 

[Waffle24]

Ah, I think I've misunderstood the question "What is the difference in height of the mercury columns in legs 1 and 2?"
So I actually need to tell the difference of each of column right?

In leg 1 : 19cmHg - 16cmHg = 3 cmHg

In leg 2 : Eh, would you like to help me on this one? Since I don't really understand the following part "At what distance below the mercury surface in leg 1 will the pressure be equal to atmospheric? The mercury level in leg 2 will be at this height. Can you see why?"

 

[mjc123]

I thought I was helping you. I don't see what you don't understand. Can you do what I suggested and draw a diagram?

 

[Waffle24]

I thought I was helping you. I don't see what you don't understand. Can you do what I suggested and draw a diagram?

On edit :

Ah I see it now, so the difference of leg 2 is 15cm Hg. Total = 3cmHg(leg 1) + 15cmHg(leg 2) = 18 cmHg has drained.

Now you can get the Volume :
V = 2 × 18
V = 36 cm^3

 

[mjc123]

I agree with your answer. Do you see why they say "a picture is worth a thousand words"?

 

[Waffle24]

I agree with your answer. Do you see why they say "a picture is worth a thousand words"?

Right, thank you so much for taking the time to help me.