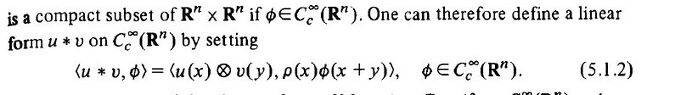Understanding Support of Convolution: Does the Equality Hold?

[evinda]

Hello! (Wave)

Let $u$ and $v$ be two distributions on $\mathbb{R}^n$, at least one of which has compact support. I have to show that $supp(u \ast v)=supp u + supp v$.

But does the equality hold? Or does it only hold that $supp(u \ast v) \subset supp u + supp v$ ?

 

[evinda]

For $supp(u \ast v) \subset supp u + supp v$ I have found the following proof:

View attachment 5401
First of all, we know that one of the $supp u, supp v$ has compact support. How do we know that the other one is closed?Furthermore, why will we have proven that $supp(u \ast v)=supp u+ supp v$, by showing that the restriction of $u \ast v$ to the open set $\mathbb{R}^n \setminus{(supp u+ supp v)}$ is $0$?

Also could you explain to me the explanation why the restriction of $u \ast v$ to the above set is $0$ ? I haven't really understood it.
Also, if equality holds could you give me a hint how to show that $supp u+ supp v \subset supp(u \ast v)$ ?

 

[evinda]

Ok, I got it.
But could you explain me the rest, i.e. the part [m] But this is immediate... $x+y \in supp u+ supp v$[/m] ?View attachment 5413