Understanding tension and centripedal force in a puck and weight

[ago01]

For practice I did the following problem:

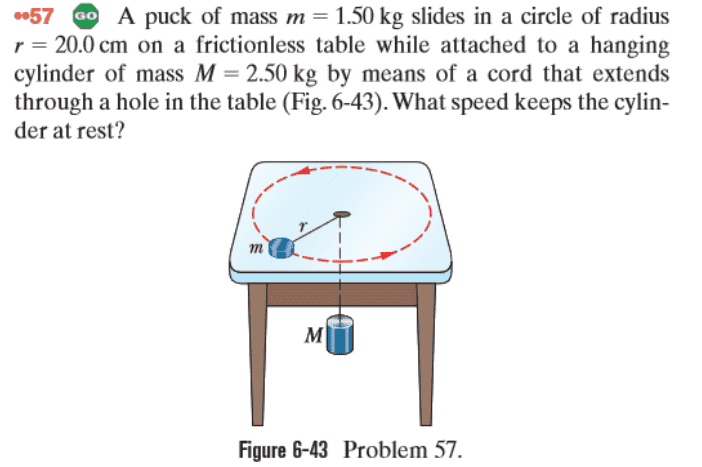
Solving this problem mechanically was simple enough using the following force diagrams:

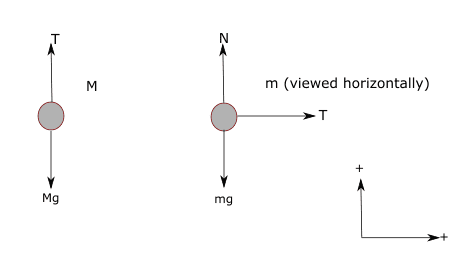Then

$$F_{net_M} = T - Mg = 0$$

Due to the stationary condition

$$T = mg$$

and

$$F_{net_m} = T = ma_c$$

$$T = ma_c$$

Because centripedal acceleration is inward the direction of the tension. The rope is pulling on the puck to stay in the circle, because without it the puck would simply fly away.

So we find after substitution:

$$Mg = m\frac{v^2}{R}$$

and after some algebra

$$v = 1.8 \frac{m}{s}$$.


So algebraically this problem wasn't terrible. Understanding the nature of the forces wasn't too bad either...at least mechanically. However I'm left wondering how exactly this tension is behaving.

Since the the rope is pulling inward on the puck it is imposing some centripedal force on the puck, and this force is causing the centripedal acceleration experienced (and what is holding the puck on the radius).

However, the rope is also pulling up on the weight. So the tension in the rope is inward facing (towards the hanging weight), yet the weight experiences some upward tension to balance out gravitational force as well! My intuition is failing me.

Is this because of the right angle it is creating? The tension is inward on the table, but upward on the weight opposite gravity. Does this have something to do with the angle it's creating? If gravity and centripedal acceleration are both inward (gravity being "down and in") I would expect the rope to be slack. I'm trying to quantify this but I am failing at coming up with a way to explain it. Which bothers me because I've seen the experiment done before.

 

[jbriggs444]

So the tension in the rope is inward facing

Can you clarify what you mean when you say that tension in a rope has a direction toward one end and away from the other?

Hint: It does not.

 

[ago01]

Can you clarify what you mean when you say that tension in a rope has a direction toward one end and away from the other?

Hint: It does not.

Sure, I'll diagram what's going on in my brain

This was my original post diagrammed. However, it appears I forgot a very important condition...

I'm not sure if this is totally correct...but it feels closer. So because the puck is spinning a circle, the changing velocity is generating a centripedal acceleration. This centripedal acceleration is the inward tension. But, the puck is also "pulling back" on the weight by being held along the radius by this acceleration.

 

[jbriggs444]

Right. The tension in the cord works both ways.

It pulls left on the corner of the hole in the table. It pulls right on the puck.
It pulls down on the corner of the hole in the table. It pulls up on the weight.

 

[ago01]

Right. The tension in the cord works both ways.

It pulls left on the corner of the hole in the table. It pulls right on the puck.
It pulls down on the corner of the hole in the table. It pulls up on the weight.

I see yep. I'm glad I asked. This is a good checkpoint for me on making sure I'm getting force pairs correctly.

Thank you!