Using Crank-Nicolson Method to solve Heat Equation

[robot1000]

I'm a bit stuck with using the C-N method

The question I'm trying to solve is the standard heat equation with:

U=[sin(pi)*x] at \tau = 0

& U = 0 at x = 0

& x = 1 for \tau \geq 0

The intervals are 0.2 in x AND 0.02 in \tau up to \tau = 0.06

I've been asked to solve using an Explicit which I've done using formula derived from the taylor theorem, but the second part is asking to use the C-N Method.

I started using this formula:

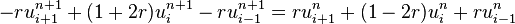in matrix form, where I'm letting r = 0.5 using

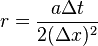
The only thing that's concerning me is that it seems a bit long winded and the answers for U(i,j) that have arisen don't seem at all close to the explicit method.

I put it all in matrix form and then using Gaussian elimination, is the correct method?

 

[robot1000]

Update 1

I've managed to work through the first matrix for u(n,1) and seem to have gotten a good set of results. What I've noticed is that the u(1,1) = u(4,1) & u(2,1) = u(3,1).

Is it worth just skipping out the 3rd and 4th row in the matrix as I can just input the results from u(1,n) and u(2,n) into u(3,n) and u(4,n)?

Update 2

I misread the question, which actually just asked for the first time step which I had already calculated.