Using repmat to plot a periodic function

[Wrichik Basu]

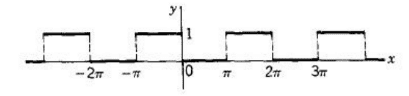
Consider the following function:
$$f(x) = \begin{cases}
1 & \text{when} & -\pi<x<0\\
0 & \text{when} & 0<x<\pi
\end{cases}$$
Beyond $-\pi$ and $\pi$, the function just repeats itself; it is periodic.

I want to plot this function for values beyond $-\pi$ and $\pi$. The graph should look something like this:

​

This answer to a similar question in MATLAB central says I have to use repmat, but I can't understand how to use it in my specific case.

Any help is appreciated.

 

[jedishrfu]

First try running the example as is.

Notice they define an f function via the @(x) scheme

Repmat then replicates the function f so you need to define a similar function for your plot maybe something like this (a guess):

f = @(x) [ 0 * (sin(x)<=0) + 1 * (sin(x)>0) ]

where x is in radians and the sin(x)<=0 and sin(x)>0 factors control the 0 1 output that you're looking for. I've not tested this though.

 

[Wrichik Basu]

First try running the example as is.

Notice they define an f function via the @(x) scheme

Repmat then replicates the function f so you need to define a similar function for your plot maybe something like this (a guess):

f = @(x) [ 0 * (sin(x)<=0) + 1 * (sin(x)>0) ]

where x is in radians and the sin(x)<=0 and sin(x)>0 factors control the 0 1 output that you're looking for. I've not tested this though.

I did something like this:

f = @(x)[1.*(-pi<x & x<0) + 0.*(0<x & x<pi)];
x = linspace(-pi,pi);
intvl = [-9 9];
pfx = repmat(f(x),1,diff(intvl)/3);
px = linspace(intvl(1),intvl(2),length(pfx));
plot(px, pfx);
hold on; grid on; grid minor;
xticks([-4*pi:1:4*pi]);
xticklabels({'-4\pi', '-3\pi', '-2\pi', '-\pi', '0', '\pi', '2\pi', '3\pi', '4\pi'});
xlim([-4*pi 4*pi]);

After executing till line 7, I get the following figure:

After executing lines 8, 9 & 10, I get this one:

Doesn't quite match the figure I want. Where is the problem?

 

[jedishrfu]

Your anonymous function looks suspicious only when x<-pi will you get a 1

Did you try the one I wrote for f = @(x) ?