mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
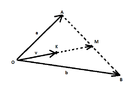
Using vector notation describe a triangle ( in space ) that has as vertices the origin and the endpoints of the vectors $\overrightarrow{a}$ and $\overrightarrow{b}$.
Could you tell me what I am supposed to do?? (Wondering)
Using vector notation describe a triangle ( in space ) that has as vertices the origin and the endpoints of the vectors $\overrightarrow{a}$ and $\overrightarrow{b}$.
Could you tell me what I am supposed to do?? (Wondering)