Vector image on another vector

[baby_1]

Hello
I want to demonstrate a equation of Vector image on another vector (A on B)

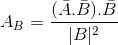
So i go this steps

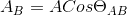
and as we know

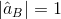
so change the equation

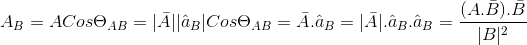
but in my equation A is (vector scale) not a (Vector)!
what is my problem?

 

[HallsofIvy]

You have $\overline{A}$, $A$, and $\left|\overline{A}\right|$. I understand that $\overline{A}$ is a vector and that $\left|\overline{A}\right|$ is its length but what is $A$?

 

[baby_1]

Thanks for your replay
A and |A| both of them are length of A vector (in electromagnetic books we assume that A=|A| for easy to write)

 

[pwsnafu]

Then pick one and stick with it. Similarly, don't swap between upper and lower case.

 

[baby_1]

I rewrite the Steps.
main formula:

steps:

as we know

and

so

but in my equation |A| is (vector length) not a (Vector)!
what is my problem?

 

[Ratch]

Oh Baby,

What are you doing? You are taking the dot product of vector A and vector B which results in a scalar. Then you are taking the dot product of that scalar with vector B. That makes no sense.

I think you want the dot product of vector A and vector B/|B|. B/|B| is the unit vector in the B direction.

Ratch

 

[baby_1]

Thanks friends
i found my probelm
Image of Vector of A on B is a Vector and we should define the direct of it when write the image equation