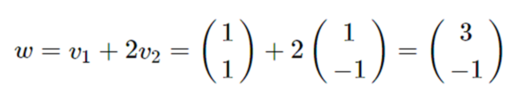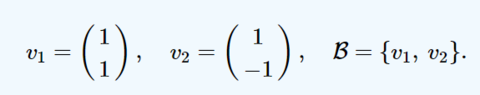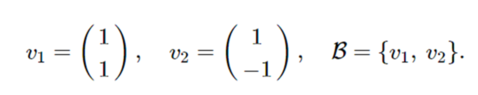- #1
fog37
- 1,568
- 108
Hello,
I have watched a really good Youtube video on linear algebra by Dr. Trefor Bazett and it made me think about a question...
()
Personal Review
A basis in 2D space is formed by any two independent vectors that are not collinear geometrically. Any vector in the 2D space can then be constructed as a linear superposition of the two basis vectors. A basis has its own coordinate system grid defined by drawing lines parallel to each basis vector. There are standard and nonstandard (non-orthogonal) bases. As soon as we draw two unit length perpendicular vector on a white page, we have implicitly created our standard basis ##E##. Any other pair of noncollinear vectors at some angle is a non-orthogonal basis...Fine.
Example:
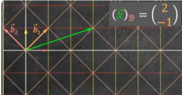
The basis ##C## is composed of basis vector ##c_1## and ##c_2## which are sketched as non-orthogonal vectors.
Such vectors have, with respect to the standard basis ##E##, the following coordinates: ##c_1= (1,-1)## and ##c_2=(0,2)## with ##C##={##c_1##, ##c_2##}:

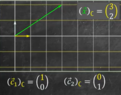
An arbitrary vector ##w## has coordinates ##(3,2)## according to basis ##C## and coordinates ##(3,1)## according to the standard basis E {##e_1## , ##e_2##}:
From the perspective of the standard basis ##E##

From the perspective of the basis ##C##
Dot product: the dot product measures if two vectors are orthogonal/perpendicular (dot product=zero equal perpendicular). From the standard basis, we sketch the basis vectors ##c_1## and ##c_2## as non orthogonal with a nonzero dot product. However, from within basis ##C##, its basis ##c_1## and ##c_2## are now perpendicular with zero dot product and the basis vectors ##e_1## and ##e_2## are now not orthogonal...
Are my conclusion correct?
Does the dot product for two arbitrary vectors change depending from the basis perspective? So the dot product is basis dependent the same as the lack or presence of geometrical perpendicularity? I imagine that if the basis vectors are not orthogonal anymore, then any other two vectors that were orthogonal is the ##E## basis will not be orthogonal in the new basis...
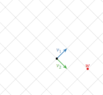
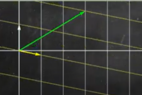
From the standard basis ##E## with its rectangular grid, the green vector below has coordinates ##(3,1)##. Coordinates are "instructions" on how to stretch the basis vectors.
I have watched a really good Youtube video on linear algebra by Dr. Trefor Bazett and it made me think about a question...
()
Personal Review
A basis in 2D space is formed by any two independent vectors that are not collinear geometrically. Any vector in the 2D space can then be constructed as a linear superposition of the two basis vectors. A basis has its own coordinate system grid defined by drawing lines parallel to each basis vector. There are standard and nonstandard (non-orthogonal) bases. As soon as we draw two unit length perpendicular vector on a white page, we have implicitly created our standard basis ##E##. Any other pair of noncollinear vectors at some angle is a non-orthogonal basis...Fine.
Example:
The basis ##C## is composed of basis vector ##c_1## and ##c_2## which are sketched as non-orthogonal vectors.
Such vectors have, with respect to the standard basis ##E##, the following coordinates: ##c_1= (1,-1)## and ##c_2=(0,2)## with ##C##={##c_1##, ##c_2##}:
An arbitrary vector ##w## has coordinates ##(3,2)## according to basis ##C## and coordinates ##(3,1)## according to the standard basis E {##e_1## , ##e_2##}:
From the perspective of the standard basis ##E##
- Its basis vectors ##e_1## and ##e_2## have coordinates ##(1,0)## and ##(0,1)##. Vector ##w## has coordinates ##(3,1)##. The basis vectors see their coordinate grid as a set of parallel and perpendicular lines.
- The basis vectors of basis ##C## have coordinates ##(1,-1)## and ##(0,2)##, they are not orthogonal, and the coordinate grid of ##B## appears slanted!
From the perspective of the basis ##C##
- Its basis vectors ##c_1## and ##c_2## have coordinates ##(1,0)## and ##(0,1)## and ##B## feels like it is the standard basis now.
- Vector ##w## has coordinates ##(3,2)## in basis ##C##. The basis vectors ##c_1## and ##c_2## see their coordinate grid as a set of parallel and perpendicular lines and they also see themselves as orthogonal while they view the basis vector of basis ##E## as non-orthogonal.
Dot product: the dot product measures if two vectors are orthogonal/perpendicular (dot product=zero equal perpendicular). From the standard basis, we sketch the basis vectors ##c_1## and ##c_2## as non orthogonal with a nonzero dot product. However, from within basis ##C##, its basis ##c_1## and ##c_2## are now perpendicular with zero dot product and the basis vectors ##e_1## and ##e_2## are now not orthogonal...
Are my conclusion correct?
Does the dot product for two arbitrary vectors change depending from the basis perspective? So the dot product is basis dependent the same as the lack or presence of geometrical perpendicularity? I imagine that if the basis vectors are not orthogonal anymore, then any other two vectors that were orthogonal is the ##E## basis will not be orthogonal in the new basis...
From the standard basis ##E## with its rectangular grid, the green vector below has coordinates ##(3,1)##. Coordinates are "instructions" on how to stretch the basis vectors.
Attachments
Last edited: