- #1
Happiness
- 679
- 30
How does (6.79) satisfy (6.70)?
After substitution, I get
$$(1-w^2)\frac{d^{l+2}}{dw^{l+2}}(w^2-1)^l-2w\frac{d^{l+1}}{dw^{l+1}}(w^2-1)^l+l(l+1)\frac{d^{l}}{dw^{l}}(w^2-1)^l$$
Using product rule in reverse on the first two terms,
$$(1-w^2)\frac{d^{l+1}}{dw^{l+1}}(w^2-1)^l+l(l+1)\frac{d^{l}}{dw^{l}}(w^2-1)^l$$
$$(1-w^2)\frac{d^{l+1}}{dw^{l+1}}(w^2-1)^l-2w\frac{d^{l}}{dw^{l}}(w^2-1)^l+2w\frac{d^{l}}{dw^{l}}(w^2-1)^l+l(l+1)\frac{d^{l}}{dw^{l}}(w^2-1)^l$$
Using product rule in reverse on the first two terms,
$$(1-w^2)\frac{d^{l}}{dw^{l}}(w^2-1)^l+2w\frac{d^{l}}{dw^{l}}(w^2-1)^l+l(l+1)\frac{d^{l}}{dw^{l}}(w^2-1)^l$$
$$\big[(1+2w-w^2)+l(l+1)\big]\frac{d^l}{dw^l}(w^2-1)^l$$
How do we prove it is equal to 0?
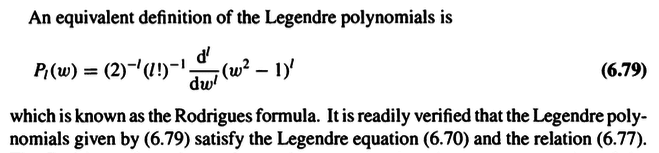
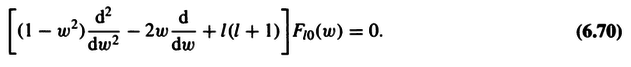


After substitution, I get
$$(1-w^2)\frac{d^{l+2}}{dw^{l+2}}(w^2-1)^l-2w\frac{d^{l+1}}{dw^{l+1}}(w^2-1)^l+l(l+1)\frac{d^{l}}{dw^{l}}(w^2-1)^l$$
Using product rule in reverse on the first two terms,
$$(1-w^2)\frac{d^{l+1}}{dw^{l+1}}(w^2-1)^l+l(l+1)\frac{d^{l}}{dw^{l}}(w^2-1)^l$$
$$(1-w^2)\frac{d^{l+1}}{dw^{l+1}}(w^2-1)^l-2w\frac{d^{l}}{dw^{l}}(w^2-1)^l+2w\frac{d^{l}}{dw^{l}}(w^2-1)^l+l(l+1)\frac{d^{l}}{dw^{l}}(w^2-1)^l$$
Using product rule in reverse on the first two terms,
$$(1-w^2)\frac{d^{l}}{dw^{l}}(w^2-1)^l+2w\frac{d^{l}}{dw^{l}}(w^2-1)^l+l(l+1)\frac{d^{l}}{dw^{l}}(w^2-1)^l$$
$$\big[(1+2w-w^2)+l(l+1)\big]\frac{d^l}{dw^l}(w^2-1)^l$$
How do we prove it is equal to 0?