Bruno Tolentino
- 96
- 0
See the image that I uploaded...
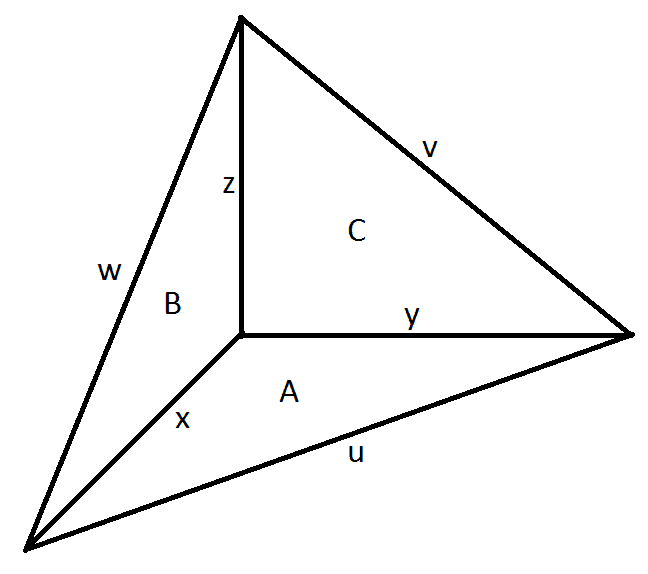
I want to write the surface S (bounded by edges u, v and w) in terms of x, y and z, u, v and w and A, B and C. And I got it!
See:
S(A,B,C) = \sqrt{A^2+B^2+C^2}
S(x,y,z) = \sqrt{\frac{1}{4}( (yz)^2 + (zx)^2 + (xy)^2 )}
S(u,v,w) = \sqrt{(+u+v+w)(-u+v+w)(+u-v+w)(+u+v-w)}
And the Volume V:
V(x,y,z) = \frac{1}{6} xyz
But, I don't know how to write V in terms of A, B, C neither u, v, w. Can you help me with this, please?
I want to write the surface S (bounded by edges u, v and w) in terms of x, y and z, u, v and w and A, B and C. And I got it!
See:
S(A,B,C) = \sqrt{A^2+B^2+C^2}
S(x,y,z) = \sqrt{\frac{1}{4}( (yz)^2 + (zx)^2 + (xy)^2 )}
S(u,v,w) = \sqrt{(+u+v+w)(-u+v+w)(+u-v+w)(+u+v-w)}
And the Volume V:
V(x,y,z) = \frac{1}{6} xyz
But, I don't know how to write V in terms of A, B, C neither u, v, w. Can you help me with this, please?