SpaceExplorer
- 25
- 0
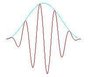
Photons are always called 'particles'. But through many experiments (by scientists such as Geoffrey Taylor), it has been found that photons show some strange characteristics which resemble those of waves. In fact scientists also reveal that electrons also show wave-like nature(in fact they have frequencies). So what can we call them-waves or particles? Or none of them? And how is the Heisenberg's uncertainty principle applicable here?