What are the best algorithms for solving a TSP with 6 points?

[mathmari]

Hey!

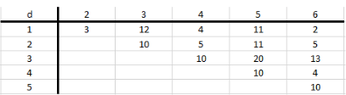
We are given the input for TSP with $6$ points with the following distances:
View attachment 5849
I want to find the approximation for a TSP-Tour using the NEAREST NEIGHBOR and the NEAREST INSERTION by starting by the vertex $1$.

Do we have the following graph from the above table?
View attachment 5851
Or do we get a directed graph? (Wondering)

Using the NEAREST NEIGHBOR we start by the vertex $1$ and then we visit at each step a non-visited vertex with the minimum distance, right? (Wondering)
So using this algorithm we get the following Tour:
$$1\rightarrow 6\rightarrow 4\rightarrow 3\rightarrow 2\rightarrow 5\rightarrow 1$$ with total distance $48$

or

$$1\rightarrow 6\rightarrow 4\rightarrow 5\rightarrow 2\rightarrow 3\rightarrow 1$$ with total distance $49$

right? (Wondering) The NEAREST INSERTION is the following:

T <- {1} 
while |T|<n do 
   j <- vertex with minimal d(T,j), j notin T 
   insert j with minimal cost into T 
return T

where $d(T,j)=\min_{i\in T}d(i,j)$ and the costs, to add $j$ between $i$ and $k$ are $\text{cost}(j)=\min_{(i,k)\in T} d(i,j)+d(j,k)-d(i,k)$

So using this algorithm we get the following:
T = {1}
j = 6 , d(1,6)=2
T = {1,6}
j = 2 , d(1,2)=3
T = {1,6,2}
j = 4 , d(1,4)=d(6,4)=4
T={1,6,2,4}
j = 3 , d(2,3)=d(4,3)=10 or j = 5 , d(4,5)=d(6,5)=10
T = {1,6,2,4,3} T = {1,6,2,4,5}
j = 5 , d(4,5)=d(6,5)=10 j = 3 , d(4,3)=d(2,3)=10
T = {1,6,2,4,3,5} T = {1,6,2,4,5,3}
with total distance $2+3+4+10+10=29$.

Is this correct? (Wondering)

 

[phymat]

Hmmm... Looks fine to me.

 

[mathmari]

Hmmm... Looks fine to me.

Thank you! (Smile)