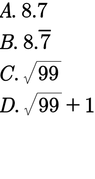What Are the Different Types of Numbers and How Can You Determine Them?

[nycmathguy]

Homework Statement

Determine whether the number is a natural number, an integer, a rational number, or an irrational number.

Relevant Equations

None

Determine whether the number is a natural number, an integer, a rational number, or an irrational number. (Some numbers fit in more than one category.) The following facts will be helpful in some cases: Any number of the form sqrt{n}
where n is a natural number that is not a perfect square, is irrational. Also, the sum, difference, product, and quotient of an irrational number and a nonzero rational are all irrational.

See attachment.

For A, I will say rational.

For B, I'm not sure because 8.(bar)7 means 8.777777...

For C, I will say irrational.

For D, I will also say irrational.

You say?

 

[PeroK]

A, C and D are correct. What about B?

Hint: infinite series.

 

[Mark44]

Hint: infinite series.

I don't think he knows about infinite series.
His textbook probably has an explanation in terms of whether the decimal representation terminates (i.e., ends with a zero) or repeats a specific, fixed-length pattern.

 

[PeroK]

I don't think he knows about infinite series.
His textbook probably has an explanation in terms of whether the decimal representation terminates (i.e., ends with a zero) or repeats a specific, fixed-length pattern.

Perhaps some lateral thinking based on shifting digits? Is this Ron Larson again?

 

[DaveE]

Hint: what if you multiply 8.7777... by 9?
I'd guess there's a 50% chance the guy that wrote this quiz doesn't know about part B either. I think this video will help:

 

[nycmathguy]

A, C and D are correct. What about B?

Hint: infinite series.

For B. I think the decimal is actually 8.777777777777777777777777777, and it is a rational number. Can this by written as 79/9?

 

[PeroK]

For B. I think the decimal is actually 8.777777777777777777777777777, and it is a rational number. Can this by written as 79/9?

If you do long division for 79/9, you get $8.777 \dots$. That would be good enough for me.

Have you studied (infinite) geometric series?

PS can you show that any repeating decimal is some whole number divided by $9, 99, 999$ etc?

 

[Mark44]

For B. I think the decimal is actually 8.777777777777777777777777777

Note that $8.777777777777777777777777777$ and $8.777777777777777777777777777\dots$ are different numbers. The latter can be written as $8.777\dots$ to mean exactly the same thing. The dots (called an ellipsis) mean that the pattern continues indefinitely.

 

[nycmathguy]

Note that $8.777777777777777777777777777$ and $8.777777777777777777777777777\dots$ are different numbers. The latter can be written as $8.777\dots$ to mean exactly the same thing. The dots (called an ellipsis) mean that the pattern continues indefinitely.

Very cool.