What are the implied domain and range of cos(arctan(x))?

[Darkmisc]

Homework Statement

The domain of cos is restricted to [0, pi]. What is the implied domain and range of cos(tan^-1(x))?

Relevant Equations

y=cos(tan^-1(x))?

Hi everyone

I have the solution to this question, but I'm not sure I understand it.

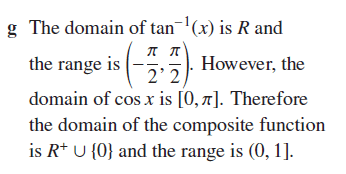
Why is the domain of the composite function

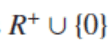and not [0, pi]?

Is it because tan^-1 (0 and R+) will always give a value between (-pi/2, pi/2)? I.e. the domain of the composite function refers to x.

Is 0 excluded from the range of the composite function because pi/2 is excluded from the domain of tan^-1?

Thanks

 

[anuttarasammyak]

I observe graph of
$$y=\cos(\arctan x)$$
shows peak y=1 at x=0 and going down to zero for both plus and minus x. x=$\pm \infty$ correspond with arctan x=$\pm \pi/2$. It should be adjusted if we apply [0,$\pi$) for x. Isn't it enough ?

 

[lurflurf]

To find the implied domain of a composite function we need to consider the inverse image of the outer function. So we If we want 0<arctan(x)<pi we must have 0<=x as the domain. Next we consider values of cos(arctan(x)) that are possible. That will be the range. 0 excluded from the range of the composite function because pi/2 is excluded from the range of tan^-1. Yes, tan^-1 ({0} U R+) will always give a value in (-pi/2, pi/2) in fact in [0, pi/2) require that arctan be in [0, pi] due to the restriction of cos.

 

[pbuk]

I have the solution to this question, but I'm not sure I understand it.

I think you do

Why is the domain of the composite functionView attachment 320662 and not [0, pi]?

Please don't use images, write $\mathbb R^+ \cup \{0\}$, or the less clunky $[0, \infty)$.

Is it because tan^-1 (0 and R+) will always give a value between (-pi/2, pi/2)?

Yes.

Is 0 excluded from the range of the composite function because pi/2 is excluded from the domain of tan^-1?

Yes.