Observe that
$a_1=1$, $a_2=2$, $a_3=3$, $a_4=5$,$a_5=7$, $a_6=10$, $a_7=13$, $a_8=17$, $a_9=21$, $a_{10}=26$, $\cdots$
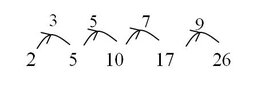
We are asked to find the last 4 digits of $a_{2012}$ term, so, if we only consider the terms $a_2=2$, $a_4=5$, $a_6=10$, $a_8=17$, $a_{10}=26$, $\cdots$, we see that
1.
the differences between the terms made up an arithemetic sequence (3, 5, 7, 9, ...), since
View attachment 1659
and hence we get the sum of the first $n$ terms of the sequence (3, 5, 7, 9,...) be
$S_n=\dfrac{n}{2}(2(3)+(n-1)(2))=n(n+2)$.
2. Once we recognize this pattern, we can easily find whichever term that we would like to, says, if we want to look for the 5th term in this sequence ($2,5,10,17,26,37,\cdots$), then what are we going to do to find that fifth term is by adding the first term, that is 2 to the sum of the first 4 terms of the arithmetic sequence (3, 5, 7, 9, ...), i.e.
$a_5=2+4(4+2)=26$
Therefore, if we look for the 1006th term in the sequence ($a_2=2$, $a_4=5$, $a_6=10$, $a_8=17$, $a_{10}=26$, $\cdots$), that means we are actually find the $a_{2012}$ of the given sequence in the original problem.
So, $a_{1006}=2+1005(1005+2)=1012037$, thus, the last four digits of $a_{2012}$ is 2037.