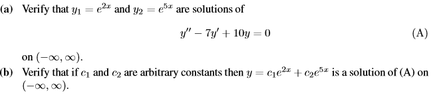SUMMARY
The discussion focuses on solving homogeneous linear equations, specifically through the method of substituting derivatives into the ordinary differential equation (ODE). The example provided involves the function \(y_1 = e^{2x}\), where the first and second derivatives are calculated and substituted into the ODE, confirming that \(y_1\) is indeed a solution. The conversation also addresses the implications of the interval of definition for solutions, clarifying that the solutions are valid for all real \(x\) unless specified otherwise.
PREREQUISITES
- Understanding of ordinary differential equations (ODEs)
- Knowledge of derivatives and their applications
- Familiarity with exponential functions
- Basic concepts of solution intervals in calculus
NEXT STEPS
- Study the method of undetermined coefficients for solving ODEs
- Learn about the existence and uniqueness theorem for differential equations
- Explore the implications of solution intervals in differential equations
- Practice solving various homogeneous linear equations using different functions
USEFUL FOR
Students preparing for exams in calculus or differential equations, educators teaching ODEs, and anyone seeking to deepen their understanding of homogeneous linear equations and their solutions.