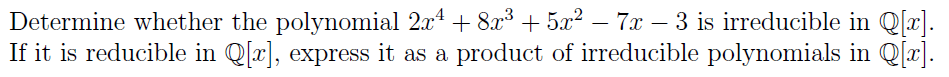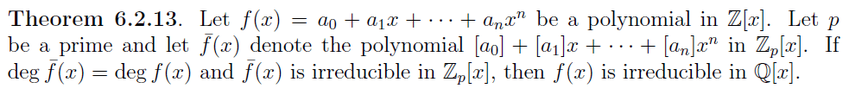What Causes Discrepancies Between Rational Root Test and Modulo p Methods?

[Joe20]

Hi all,

I have done the question in two methods. The first method is done by rational root test and the second method is by modulo p (theorem is as attached). It seems that my answers for both methods do not tally.

1. Where have I done wrong in the attached for the methods? Which is the correct presentation of answer for this question (i.e. rational test method or modulo p ?
2. How do I tell when to use rational root test method or modulo p method? When modulo p method not applicable?

Your advise is greatly appreciated. Thanks.

 

[Opalg]

Your Theorem 6.2.13 says that if $\deg \overline{f}(x) = \deg f(x)$ and $\overline{f}(x)$ is irreducible in $\Bbb{Z}_p[x]$ then $f(x)$ is irreducible in $\Bbb{Q}[x]$. The theorem does not tell you anything at all about what might happen when $\overline{f}(x)$ is reducible in $\Bbb{Z}_p[x]$. So the fact that your $\overline{f}(x)$ is reducible in $\Bbb{Z}_3[x]$ does not imply that ${f}(x)$ is reducible in $\Bbb{Q}[x]$. That would amount to saying that the converse of Theorem 6.2.13 is true, which is certainly not the case.

The technique of looking at $\overline{f}(x)$ in $\Bbb{Z}_p[x]$ is a one-way test. You can use it to prove irreducibility of $f(x)$, but you cannot use it to prove reducibility.

Your argument using the rational root test is correct, and shows that $f(x)$ is irreducible in $\Bbb{Q}[x]$.

 

[Joe20]

Thank you for the advice.

I have one more question. Can you kindly help me to check if the argument or reasoning stated in the last part of the rational root test method is correct? ( from this " f(x) has no linear factor, hence 2x^2+2x -3 ... till hence 2x^4+8x^3+5x^2-7x-3 = (2x^2+2x -3)(x^2+3x+1).

Thanks.

 

[Opalg]

Thank you for the advice.

I have one more question. Can you kindly help me to check if the argument or reasoning stated in the last part of the rational root test method is correct? ( from this " f(x) has no linear factor, hence 2x^2+2x -3 ... till hence 2x^4+8x^3+5x^2-7x-3 = (2x^2+2x -3)(x^2+3x+1).

Sorry, I forgot that your rational root investigation actually showed that $2x^4+8x^3+5x^2-7x-3$ is reducible in $\Bbb{Q}[x]$. You correctly showed that $2x^4+8x^3+5x^2-7x-3 = (2x^2+2x -3)(x^2+3x+1).$

 

[Joe20]

I am somehow confused by the question with this statement " if it is reducible in Q[x], express it as a product of irreducible polynomials in Q[x]. "

1. Does the part "if it is reducible in Q[x]" refers to any factorization [i.e. like the case of 2x^4+8x^3+5x^2−7x−3=(2x^2+2x−3)(x^2+3x+1) ] without the need to solve for the x value to check if it rational or irrational? Then the next question is how does this apply to reducible in Q[x]?

2. The next part " express it as a product of irreducible polynomials in Q[x]. " refers to (2x^2+2x−3) and (x^2+3x+1) being degree 2 and no roots to each quadratic polynomial?

3. So it also implies that if the polynomial is irreducible, then I can't even get to any form of factorization, hence needless to say any product of polynomials. Am I correct to say that?

Thanks.

 

[Joe20]

Sorry, I forgot that your rational root investigation actually showed that $2x^4+8x^3+5x^2-7x-3$ is reducible in $\Bbb{Q}[x]$. You correctly showed that $2x^4+8x^3+5x^2-7x-3 = (2x^2+2x -3)(x^2+3x+1).$

I am somehow confused by the question with this statement " if it is reducible in Q[x], express it as a product of irreducible polynomials in Q[x]. "

1. Does the part "if it is reducible in Q[x]" refers to any factorization [i.e. like the case of 2x^4+8x^3+5x^2−7x−3=(2x^2+2x−3)(x^2+3x+1) ] without the need to solve for the x value to check if it rational or irrational? Then the next question is how does this apply to reducible in Q[x]?

2. The next part " express it as a product of irreducible polynomials in Q[x]. " refers to (2x^2+2x−3) and (x^2+3x+1) being degree 2 and no roots to each quadratic polynomial?

3. So it also implies that if the polynomial is irreducible, then I can't even get to any form of factorization, hence needless to say any product of polynomials. Am I correct to say that?

Thanks.