What divisor does Microsoft Excel use for standard deviation?

[ssd]

By definition standard deviation has divisor 'N' .

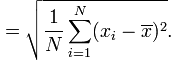
But in Microsoft Excel the "STDEV" function gives 'N-1' as divisor.
This may not be major issue to many of the people. But the command "STDEV"
makes many users feel that this is standard deviation, i.e. it has divisor 'N'. Misleading...is not it?

 

[EnumaElish]

"the square root of the bias-corrected variance [estimator] is sometimes also known as the standard deviation"

http://mathworld.wolfram.com/StandardDeviation.html

 

[statdad]

In texts you will see the one with divisor N defined as the population standard deviation: the one with divisor N-1 is referred to as the sample standard deviation.

There is no single "standard deviation formula" - the appropriate formula depends on context.

 

[CRGreathouse]

Excel has STDEV, the sample standard deviation, and STDEVP, the population standard deviation. Usually you want the sample standard deviation, which is why the commands are named as they are.

I'm pretty sure this is all in the Excel help.

 

[ssd]

At the very outset of this reply let me say that all of you are correct from your
respective point of view. But my point was a little different which EnumaElish has got almost correctly.
To clarify my point I will say a word or two.

"the square root of the bias-corrected variance [estimator] is
sometimes also known as the standard deviation"
http://mathworld.wolfram.com/StandardDeviation.html

True. You rightly got it: "sometimes" not in general- or I may say, not commonly.
That is why I used the term "misleading" instead of "bugged".

Excel has STDEV, the sample standard deviation,
and STDEVP, the population standard deviation. Usually you want the sample
standard deviation, which is why the commands are named as they are.

Point well taken.

In texts you will see the one with divisor N defined as the population
standard deviation: the one with divisor N-1 is referred to as the sample standard deviation.
There is no single "standard deviation formula" - the appropriate formula depends on context.

In the first step of stating the descriptive measures of dispersion all the textbooks, as I have gone through
( ex: attachment -1), use a single and unique "standard deviation formula" (and no context dependent definition). And this is done much before coming to the chapters of "point estimation" or "sample survey" (where we start talking about "expectation/unbiasedness" or "population/sample".

Then again, as learned from textbooks( attachment-2), the sample variance (also) have divisor
n, not n-1). Hence it is stated, sample variance is not unbiased estimator of population variance.

attachment -1

attachment-2

 

[statdad]

The standard deviation with the divisor of n is the MLE when the Gaussian model is assumed and both $$\mu$$ and [/tex] \sigma [/tex] are unknown. (It is a function of the variance, the MLE of $$\sigma ^2$$, so is the MLE of the standard deviation. The sample variance with the divisor of n -1 comes from the unbiased estimator of variance.

But: this expression
$$\frac 1 n \sum_{i=1}^n (x_i-\bar x)^2,$$

are also given as formulas for population variance and sample variance, respectively, for discrete populations, since in this case the population mean is defined as

$$\mu = \sum 1 n \sum_{i=1}^n$$

and so is identical in form to the arithmetic mean.

So, when you use the variance with n in the denominator, you must be clear whether you are dealing with a sample or population: the interpretation differs. That is the context.

 

[ssd]

The standard deviation with the divisor of n is the MLE when the Gaussian model is assumed and both $$\mu$$ and [/tex] \sigma [/tex] are unknown. (It is a function of the variance, the MLE of $$\sigma ^2$$, so is the MLE of the standard deviation. The sample variance with the divisor of n -1 comes from the unbiased estimator of variance.

But: this expression
$$\frac 1 n \sum_{i=1}^n (x_i-\bar x)^2,$$

are also given as formulas for population variance and sample variance, respectively, for discrete populations, since in this case the population mean is defined as

$$\mu = \sum 1 n \sum_{i=1}^n$$

and so is identical in form to the arithmetic mean.

So, when you use the variance with n in the denominator, you must be clear whether you are dealing with a sample or population: the interpretation differs. That is the context.

Agree. But my point differs a little from yours.

What if you are given with 20 no.s and asked to find their mean, variance, skewness and kurtosis... without any reference to population/estimation. Remember what we did in our stating course of descriptive statistics. What I am trying to say is that, there are situations when one can look upon variance as a purely descriptive measure (of dispersion). And this measure itself is meaningful some times (apart from the fact that this measure will be used for inferential data analysis).

 

[statdad]

"without any reference to population/estimation" - I can't imagine why you you would want any set of statistics without wondering about any descriptive or inferential purpose (unless it is simply an exercise in calculation) - but so be it.

 

[ssd]

"without any reference to population/estimation" - I can't imagine why you you would want any set of statistics without wondering about any descriptive or inferential purpose (unless it is simply an exercise in calculation) - but so be it.

Right. I was more concerned about my students who are going through the initial stages of learning descriptive statistics. Most of them (if not all) use excel for their course work.