What does 3-dimensional space deform into, in the presence of gravity?

[jaketodd]

I have no expertise in this area, other than rudimentary concepts. The following might apply if the visualization of space, as depicted below, represents actual reality, but I don't know for sure. Please help me understand better, you guys!

2-dimensional space
The curvatures deform into the 3rd dimension, as can be seen in the picture below.

So in 3-dimensional space, what does space deform into? 4th!?
We can't even visualize it! Unless it doesn't deform into the 4th, but instead just stretches space, without a deformation into a 4th. See another picture below.

This is mentioned by Brian Greene, notable for his documentary The Elegant Universe. He's mostly about string theory but poses this question as well.

https://en.wikipedia.org/wiki/Curved_space

 

[PeterDonis]

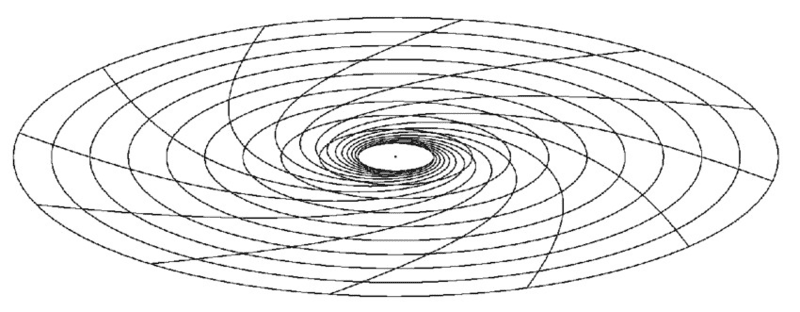
2-dimensional space
The curvatures deform into the 3rd dimension

No, they don't. The third dimension in the picture has no relationship to any dimension in reality. A curved space doesn't deform "into" anything. The curvature is intrinsic.

So in 3-dimensional space, what does space deform into?

Nothing. See above.

This is mentioned by Brian Greene, notable for his documentary The Elegant Universe.

This is a pop science source and is not a valid reference. In fact, Greene's pop science books and videos are particularly bad because of the number of misunderstandings they create among unsuspecting lay people. We have had many past PF threads on this.

 

[PeterDonis]

@jaketodd, you apparently have failed to take my advice to learn from textbooks and peer-reviewed papers instead of pop science sources. You really, really, really, really need to take it.

 

[PeterDonis]

The OP is based on a misconception obtained from an invalid pop science reference. Thread closed.