What does an off center applied torque do?

[Seppe87]

I know that if a force is applied off center (as in: not in the center of gravity), one can split them up in an equal force and a moment in/about the center of gravity. But what about a torque applied offcenter?

Maybe this image clarifies my problem:

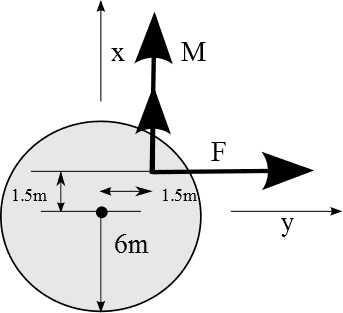
So the force will be split op in a force-moment couple at the center of gravity... But what to do with the applied torque? (Or moment, depends on how you look at things)

 

[mfb]

The effect of a torque (without a net linear force) does not depend on the position where you apply it. It leads to the same angular acceleration everywhere.

 

[Seppe87]

And what about the stresses? I can imagine that the left side of the cross section is experiencing more stress in this case than if the torque would be applied in the center.

 

[Seppe87]

Okay, I redrew the whole thing, now with correct axes.

Here I already split the force in a force in the centroid and a moment around the centroid. My question is: How do I find the maximum stress in this cross section? Where is it going to fail first? I want to know how thick my walls have to be depending on the y-value of the application point.

 

[mfb]

If you apply the force to a single point, I would expect maximum stress at this point (in addition to the center, if it is fixed there).

 

[Travis_King]

Does that moment arrow imply that there is a moment being put onto the disc about that point, into the page?

 

[Seppe87]

the moment arrow represents the axis around which the moment is acting. Using the right-hand rule, one can see that the left must be in tension and the right in compression.

 

[AlephZero]

How do I find the maximum stress in this cross section? Where is it going to fail first? I want to know how thick my walls have to be depending on the y-value of the application point.

That depends on how the object is restrained. I guess you know what problem you are trying to solve, but just drawing a circle doesn't give us much information. You mentioned the thickness of "walls" but it isn't clear what they are from your drawing.

I'm still confused about your "momemt" arrow with two heads. Is it supposed to be a moment parallel to the Y axis, so the left hand side of the "circle" is trying to move in towards us out of the X-Y plane and the right hand side is trying to move away from us?

If you apply the force to a single point, I would expect maximum stress at this point (in addition to the center, if it is fixed there).

True, and usually the stress field is singular where the point load is applied, so the stress there is "infinite". But since point forces and moments don't exist in the real world, this is not necessarily a real-world problem.

 

[Seppe87]

@AlephZero: All that is known about the structure is that it's thin-walled, the radius, yield strength and values for F and M are known as well... There is no information about how (or if) it's restrained. The thickness of the walls is the thickness of the circle, the thickness of the black line.
About the moment. Yes, all to the left is 'coming towards you' and to the right 'away from you'. I think I solved it. I originally wanted to create a function that would plot the maximum stress at any given point of the circle. But that was too much work if I only need the know what the maximum value is. So I thought about the places where maximum stress could occur: most left side due to the moment applied or the top side due to the force applied and its induced moment. So I calculated stresses in these two points and found that the top would be most prone to failure. Thanks all for your help!