What Does the Graph of This Vector Equation Look Like?

  • Context: MHB 
  • Thread starter Thread starter ineedhelpnow
  • Start date Start date
  • Tags Tags
    Vector
Click For Summary

Discussion Overview

The discussion revolves around the graph of a vector equation given by \( r(t) = e^{2t} \mathbf{i} + e^{r} \mathbf{j} \). Participants explore the nature of the curve, potential relationships between the components, and the implications of the graph's shape.

Discussion Character

  • Exploratory
  • Mathematical reasoning
  • Debate/contested

Main Points Raised

  • Initial inquiry about the graph of the vector equation and whether a simpler equation can be derived.
  • Some participants suggest that the y-component should be \( e^t \) instead of \( e^r \), leading to a potential relationship where \( x = e^{2t} \) and \( y = e^t \).
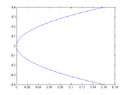
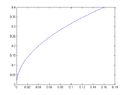
  • A participant proposes the relationship \( x = y^2 \) based on the corrected components.
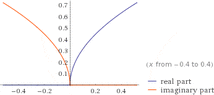
  • Discussion about the meaning of a red line in an attached graph, with clarification that it is imaginary and should be ignored, while the blue part represents \( x = y^2 \).
  • Concerns are raised about the possibility of \( y = e^t \) being negative, prompting further reflection on the nature of the graph.
  • Participants share graphical outputs from MATLAB, expressing uncertainty about the accuracy of their results.

Areas of Agreement / Disagreement

There is no consensus on the implications of the graph or the nature of the components, as participants express differing views on the y-component and its relationship to the x-component.

Contextual Notes

Participants have not fully resolved the implications of the vector equation, particularly regarding the y-component and its potential negative values. The discussion includes references to graphical representations that may not fully capture the mathematical relationships discussed.

ineedhelpnow
Messages
649
Reaction score
0
sketch the plane curve with the given vector equation

$r(t)=e^{2t}$i $+e^{r}$j

what does the graph of this look like. is there any way to get a simple equation out of the two?
 
Physics news on Phys.org
ineedhelpnow said:
sketch the plane curve with the given vector equation

$r(t)=e^{2t}$i $+e^{r}$j

what does the graph of this look like. is there any way to get a simple equation out of the two?

Can it be that the y-component should be $e^t$? :confused:

If so, suppose you define $x=e^{2t}$ and $y=e^t$.
What kind of relationship can you deduce from that? (Wondering)
 
oops. yeah the y component is e^t not e^r

- - - Updated - - -

$x=y^2$?
 
ineedhelpnow said:
oops. yeah the y component is e^t not e^r

- - - Updated - - -

$x=y^2$?

Yep! :D

What would the graph look like? (Wondering)
 

Attachments

  • MSP982220ib93c4571g25e00000eca3402f9317713.gif
    MSP982220ib93c4571g25e00000eca3402f9317713.gif
    3.6 KB · Views: 80
ineedhelpnow said:
https://www.physicsforums.com/attachments/3102

Hmm... what would be the meaning of that red line?
What kind of standard graph would it be anyway? (Wondering)
 
red line is imaginary. ignore that part. the blue part represents x=y^2
 
ineedhelpnow said:
red line is imaginary. ignore that part. the blue part represents x=y^2

Yeah right!

be-rational-get-real.png
 
dude come on... grow up (Giggle)

- - - Updated - - -

or should i say get real...
 
  • #10
ineedhelpnow said:
https://www.physicsforums.com/attachments/3102

That's what I got,using matlab:

View attachment 3104

(Blush)
 

Attachments

  • matt.png
    matt.png
    1.8 KB · Views: 104
  • #11
evinda said:
That's what I got,using matlab:

View attachment 3104

(Blush)

But... but... how can $y=e^t$ be negative?? :confused:

It does look like some standard graph, doesn't it? (Wondering)
 
  • #12
I like Serena said:
But... but... how can $y=e^t$ be negative?? :confused:

It does look like some standard graph, doesn't it? (Wondering)

I tried it again.. (Wasntme)

View attachment 3105

Is it better now? (Blush)
 

Attachments

  • matt.png
    matt.png
    1.6 KB · Views: 94
  • #13
evinda said:
I tried it again.. (Wasntme)

https://www.physicsforums.com/attachments/3105

Is it better now? (Blush)

It's perfect! (Nod)
 

Similar threads

MHB Limit of Newton's Law of Cooling....2
  • · Replies 3 ·
Replies
3
Views
1K
Undergrad Struggling with vector calculus identity used in E&M derivation
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Equivalence of alternative definitions of conservative vector fields and line integrals in different metric spaces
  • · Replies 3 ·
Replies
3
Views
3K
Undergrad Gradient Vectors: Perpendicular to Level Curves
  • · Replies 4 ·
Replies
4
Views
2K
MHB How Do You Sketch Position and Tangent Vectors for a Vector Function?
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Moving the graph to the right -- What do you think?
  • · Replies 3 ·
Replies
3
Views
3K
MHB 243.13.01.18 motion of a particle
  • · Replies 14 ·
Replies
14
Views
5K
Undergrad How to find the maximum arc length of this equation?
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Questions about these Trigonometry Graphs involving sin() and cos()
  • · Replies 3 ·
Replies
3
Views
2K
Graduate The ``kinematic equation'' of fluid flows
  • · Replies 13 ·
Replies
13
Views
2K