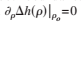SUMMARY
The discussion focuses on the interpretation of a mathematical equation involving a Monge parameterization height function, h(p), which is dependent on the radius (p). The boundary conditions specified include h(pi)=0 for the inner boundary and p0 as the outer boundary. Participants analyze the partial derivative with respect to ρ, evaluated at ρ=ρ0, and debate the appropriateness of using d/dp versus d/dρ as the differential operator. The consensus suggests that the equation's formulation is reasonable, although some uncertainty remains regarding the author's notation.
PREREQUISITES
- Understanding of Monge parameterization in differential equations
- Familiarity with boundary conditions in mathematical modeling
- Knowledge of partial derivatives and their applications
- Basic concepts of differential operators in calculus
NEXT STEPS
- Research Monge parameterization techniques in differential equations
- Study boundary value problems and their significance in mathematical modeling
- Learn about the application of partial derivatives in physics and engineering
- Explore the differences between various differential operators, particularly d/dp and d/dρ
USEFUL FOR
Mathematicians, physicists, and engineers who are working with differential equations, boundary value problems, or those interested in advanced calculus concepts.