What Edges Are Selected in the Bellman-Ford Algorithm?

[evinda]

Hello! (Wave)

I am reading an example about the Bellman-Ford algorithm in order to understand it, but I don't really know what edges we pick from the second step and at the following ones.

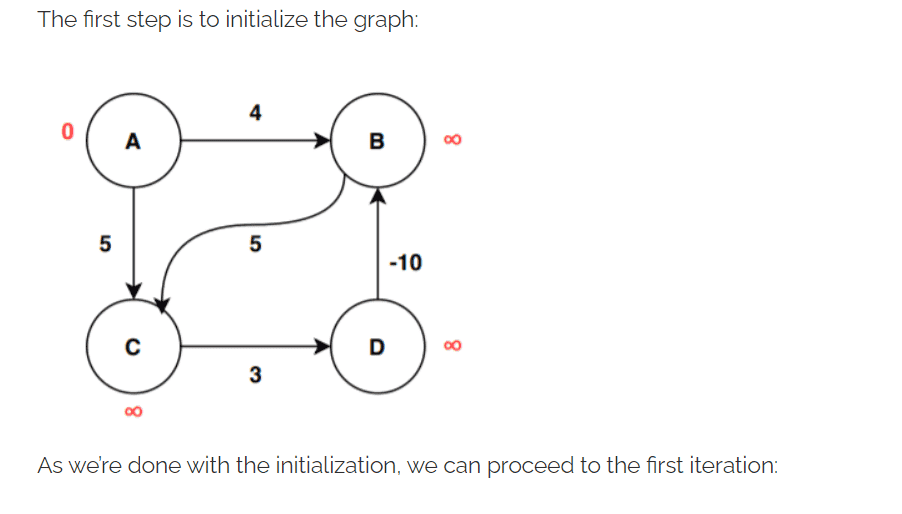
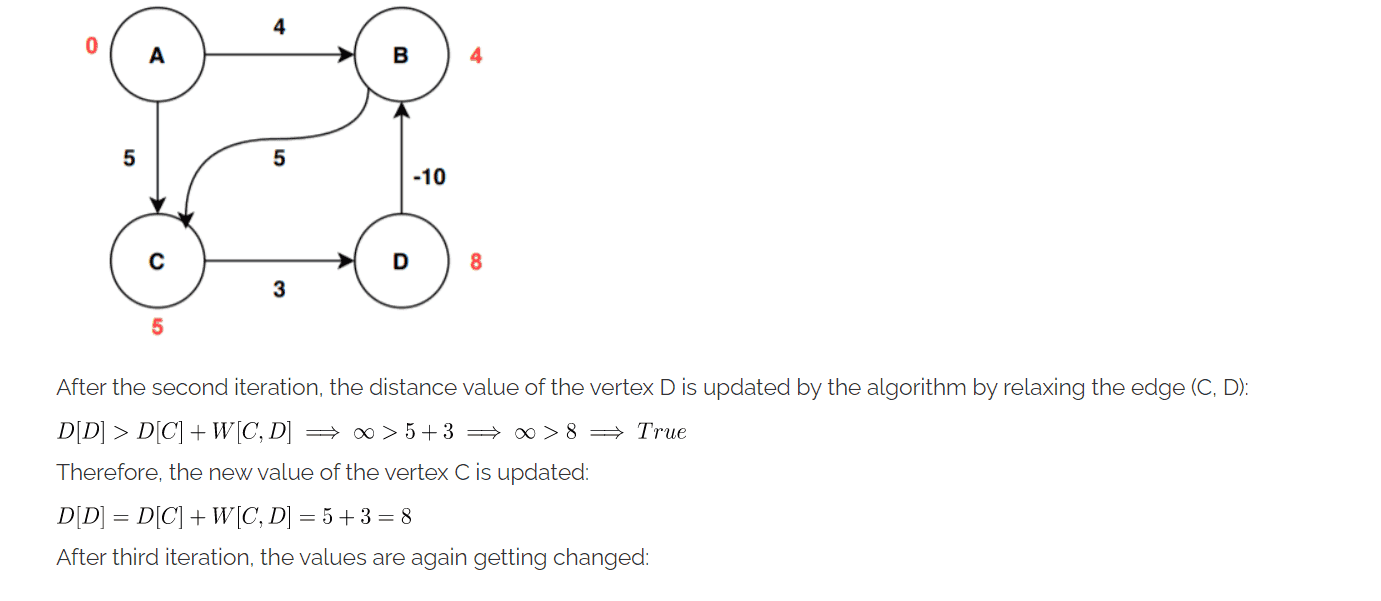
Here is the example I am looking at, where they want to detect if there is a negative cycle.

Could you explain to me the idea that we follow? (Thinking)

 

[I like Serena]

I am reading an example about the Bellman-Ford algorithm in order to understand it, but I don't really know what edges we pick from the second step and at the following ones.

Here is the example I am looking at, where they want to detect if there is a negative cycle.

Could you explain to me the idea that we follow?

Hi evinda!

Wiki explains:

Like Dijkstra's algorithm, Bellman–Ford proceeds by relaxation, in which approximations to the correct distance are replaced by better ones until they eventually reach the solution. In both algorithms, the approximate distance to each vertex is always an overestimate of the true distance, and is replaced by the minimum of its old value and the length of a newly found path.​

However, Dijkstra's algorithm uses a priority queue to greedily select the closest vertex that has not yet been processed, and performs this relaxation process on all of its outgoing edges; by contrast, the Bellman–Ford algorithm simply relaxes ''all'' the edges, and does this$|V|-1$ times, where $|V|$ is the number of vertices in the graph.​

but I don't really know what edges we pick from the second step and at the following ones.

We pick all edges and see if we can make reduce the value of the target node of each edge.

 

[evinda]

Hi evinda!

Wiki explains:

Like Dijkstra's algorithm, Bellman–Ford proceeds by relaxation, in which approximations to the correct distance are replaced by better ones until they eventually reach the solution. In both algorithms, the approximate distance to each vertex is always an overestimate of the true distance, and is replaced by the minimum of its old value and the length of a newly found path.​

However, Dijkstra's algorithm uses a priority queue to greedily select the closest vertex that has not yet been processed, and performs this relaxation process on all of its outgoing edges; by contrast, the Bellman–Ford algorithm simply relaxes ''all'' the edges, and does this$|V|-1$ times, where $|V|$ is the number of vertices in the graph.​

We pick all edges and see if we can make reduce the value of the target node of each edge.

I see... Thank you! (Mmm)