zrek said:
Yes, I think you get it right what I mean.
I suppose that ##\omega##+1 means the first transfinite ordinal "right after" ##\omega##. The set supposed to be well ordered. Therefore ##\omega## is right before ##\omega##+1. This can be (or can not, if we decide to ban this notation) also notated by the other way, using the minus sign. Say X=##\omega##+2 , then X-1=##\omega##+1 and X-2=##\omega## ... but then what is X-3 or ##\omega##-1?
This is the point where I'm confusing, the ordinal "right before" omega, this is the point where (maybe) we can't continue the order backwards.
A couple of things:
1) First, let's remember what "after" and "before" mean in this context (I'll just assume we're working with von Neumann ordinals). ##x## is after ##y##, that is, ##x > y## iff ##y \in x##; we also say in this case that ##y## is before ##x##.
2) Now, given an ordinal ##x##, how do we define the successor of ##x##, namely ##x+1##? Simple: ##x+1 = x \cup \{x\}##. Notice that this respects the definition of order given above; it also implies that if one ordinal is the successor of the other, there is no ordinal between them.
3) It's also possible to define addition of ordinals. This is a bit more complicated, but the rough idea is the following: ordinal numbers encode information about well-orders in certain sets. For instance, ##\omega## encodes information about the well-order of the natural numbers, ##\omega + \omega## about the well-order of, e.g., this set: {0, 2, 4, 6, ..., 1, 3, 5, ...} (where every even number comes before every odd number and the even and odd numbers are ordered in the usual way among themselves). So addition of ordinals encodes information about what happens when we concatenate the orders. In the previous example, ##\omega + \omega## encodes information about what happens when we concatenate the order of the even numbers with the order of the odd numbers. More formally, if ##(A, <), (B, \prec)## are well orders, their concatenation, ##C##, is defined as ##(\{0\} \times A) \cup (\{1\} \times B)##, and such that, for any ##(i, x), (j, y) \in C##, ##(i, x) < (j, y)## iff (a) ##i=j=0## and ##x < y##, (b) ##i=0## and ##j=1##, or (c) ##i=j=1## and ##x \prec y##. If ##A## and ##B## are ordinals, then ##C## is their sum. It's not difficult to see that this will give the correct results, and that in particular it agrees with our definition of successor. Notice that ordinal addition is associative, but not commutative.
4) On the other hand, this means that, in general, subtraction is not a well defined operation on the class of ordinals. In particular, we would want something like the following to hold:: ##a-b = c## iff ##a = c+b##. But, as some posters have already said, a single ordinal can be the result of many different sums, i.e. ##1+\omega=2+\omega=\omega##, but clearly ##\omega - \omega## is neither ##1## nor ##2##!
5) Finally, about well-orderings. Note that, if ##(A, <)## is a well order, that does not mean that ##(A, >)## is a well order. In fact, this can only happen with finite sets; here's a theorem: ##(A, <)## and ##(A, >)## are both well orders iff ##A## is finite. Indeed, this property is, in some contexts, taken as the definition of finite sets!
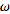 ,
,
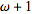 ,
,
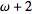 , ...
, ...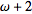 is after
is after
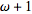 therefore
therefore
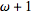 is before
is before
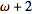 .
. ?
?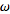 -1
-1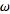 is the first transfinite ordinal, then
is the first transfinite ordinal, then
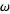 -1 should be the last finite ordinal, which simply does not exist.
-1 should be the last finite ordinal, which simply does not exist.