What is Omega: Definition and 74 Discussions

Omega (capital: Ω, lowercase: ω; Greek ὦ, later ὦ μέγα, Modern Greek ωμέγα) is the 24th and final letter in the Greek alphabet. In the Greek numeric system/Isopsephy (Gematria), it has a value of 800. The word literally means "great O" (ō mega, mega meaning "great"), as opposed to Ο ο omicron, which means "little O" (o mikron, micron meaning "little").In phonetic terms, the Ancient Greek Ω is a long open-mid o [ɔː], comparable to the vowel of English raw. In Modern Greek, Ω represents the mid back rounded vowel /o̞/, the same sound as omicron. The letter omega is transcribed ō or simply o.
As the final letter in the Greek alphabet, omega is often used to denote the last, the end, or the ultimate limit of a set, in contrast to alpha, the first letter of the Greek alphabet; see Alpha and Omega.

View More On Wikipedia.org
Recent contents Top users
  1. docnet

    Prove that f is constant on omega

    ##f(z)## is holomorphic on ##\Omega## so f(z) satisfies the C.R. equations, i.e., for ##f(z)=u+iv## ##u_x=v_y## ##u_y=-v_x## and for ##-f(z)=-u-iv## ##u_x=v_y \Rightarrow -u_x=-v_y## ##u_y=-v_x\Rightarrow -u_y=v_x## so -f(z) satisfies the C.R. equations and hence ##-f(z)## is holomorphic...
  2. Haorong Wu

    How to distinguish r and gamma, w and omega, v and nu?

    How to distinguish ##r## and ##\gamma##, ##w## and ##\omega##, ##v## and ##\nu## and ##\upsilon##? They look very similar. Are there some rules that I should use one of them in some specific cases?
  3. K

    I Why do some mesons have = sign while others have ≈ in their composition?

    Hello! I am reading Modern Particle Physics by Mark Thomson and in chapter 9.6.2 he writes the composition of certain mesons. However for some of them he uses an equality sign: $$|\rho^0> = \frac{1}{\sqrt{2}}(u\bar{u}-d\bar{d})$$ while for others he writes: $$|\omega> \approx...
  4. L

    Angular momentum L=rxP and L=I x omega ?

    When do we use L=r x P and L=I x Omega (angular velocity)? in old 8.01x - Lect 24, I pasted here link of the lecture, which will take you at exact time (at 27:02)he says "spin angular momentum" in classical physics lecture and why? I expected to hear "angular momentum" vector. Normally...
  5. T

    I Simple harmonic oscillators on floating object in liquid

    How can I find omega on an object that is floating on water which is moving up and down on the object? The problem goes by giving you a cylindrical object with radius r and height H, pw(density of water), pc(density of circle) and x(t)=a*cos(wt). I do not understand why pw*pi*r^2*dg=pc*pi*r^2Hg
  6. Alex Paul

    Equivalence of torque & angular velocity transfer function

    Hello all, I was doing some behavioural modelling of the torque transfer characteristics of a belt drive system from the driver pulley to the driven pulley. While doing the same, i have tried to see how the angular velocity is getting transferred as well. I would explain my point with the...
  7. nomadreid

    I Hilbert's omega rule, induction, omega-consistency

    As I understand Hilbert's omega rule for a first-order proposition P over the natural numbers, P(0) &P(1) &P(2) &... ⇒ ∀n∈ℕ P(n) :star: which seems to be the same as ω-consistency. Is there a difference? Further, the axiom schema of induction has each axiom for a proposition P over the...
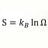
  8. morrobay

    B Clarification : S = K ln W and S = K ln omega

    With S = K ln W where W is probability system is in the state it is in relative to all other possible states : W = VN , V = volume, N = number of particles so ln W = N (ln V) And this expression is for non equilibrium state. For equilibrium state S = K ln Ω Then is the only difference between...
  9. Ranku

    I Inflation & Ω: Dark Matter & Energy Impact

    Inflation leads to Ω=1. But we also have Ωmatter+Ωdark matter+Ωdark energy = 1. So if there were no dark energy and dark matter present in the universe, would Ω have eventually deviated away from 1?
  10. E

    I Dispersion: expansion of wavenumber as function of omega

    Hi! Dealing about wave propagation in a medium and dispersion, wavenumber k can be considered as a function of \omega (as done in Optics) or vice-versa (as maybe done more often in Quantum Mechanics). In the first case, k (\omega) \simeq k(\omega_0) + (\omega - \omega_0) \displaystyle \left...
  11. Vitani11

    How Does a Cycloidal Path Ensure Isochronous Oscillations in a Pendulum?

    Homework Statement A pendulum is suspended from the cusp of a cycloid cut in a rigid support. The path described by the pendulum bob is cycloidal and is given by x = a (φ − sin φ), y = a (cos φ − 1), where the length of the pendulum is l = 4a, and where φ is the angle of rotation of the circle...
  12. D

    Bug moving on a turntable rotating with constant omega

    Homework Statement A cockroach crawls with constant speed in a circular path of radius b on a phonograph turntable rotating with constant angular speed omega. The circle path is concentric with the center of the turntable. If the mass of the insect is m and the coefficient of static friction...
  13. W

    I Difference between omega 0 and omega k

    As I try and read cosmology literature with the eyes of layman , I find two different terms that seem to represent the curvature ( or lack of) of the universe . These are omega sub zero and omega k. But I can't see the difference between the two. Can anyone explain this?
  14. zrek

    I What is before the first transfinite ordinal, omega?

    Omega is the first transinite ordinal in the set of 0, 1, 2, ..., , , , ... This set is well ordered, so is after therefore is before . What is before ? Options: 1. -1 This is confusing, since if is the first transfinite ordinal, then -1 should be the last finite ordinal, which simply...
  15. KingDaniel

    How to get frequency, w (omega), when calculating reactance

    Hi, I came across a question from our weekly set of questions that involved finding the inductive reactance and capacitive reactance, ie: XL = jwL and XC = 1 / jwC. In the solution sheet, the professor wrote that the frequency, w (omega) = 10000, however, in the question sheet, it was nowhere...
  16. Garlic

    Omega Baryon Decay: Why Create Unnecessary Particles?

    Hello, Why is there a decay mode of omega baryon that creates unnecessary particles? sss -> uds + u(bar)s and why not just sss -> dss ?
  17. F

    How Does Omega Squared Equal k/m in Simple Harmonic Motion?

    I was doing the differential equation of simple harmonic motion. At a time, to bring the equation, it simply said k/m=ω2 How does it come? Is there any proof?
  18. Dilatino

    Why can the omega meson not decay to 3 neutral pions?

    What reasons prevent the decay $\omega \rightarrow \pi^0 \pi^0 \pi^0$ from happening?
  19. davenn

    Omega Centauri: Amazing Image from 2-Month Clear Night

    one from last weekend, first clear weekend nite in 2 months Omega Centauri is the brightest globular cluster in the sky. Its an easy naked eye visible object from a reasonably dark site Canon 5D3, 30sec exp, 100-400mm @ 400mm f5.6, ISO2000 cheers Dave
  20. diegzumillo

    Entropy as log of omega (phase space volume)

    Homework Statement I've seen this problem appear in more than one textbook almost without any changes. It goes like this: Assume the entropy ##S## depends on the volume ##\bar{\Omega}## inside the energy shell: ##S(\bar{\Omega})=f(\bar{\Omega})##. Show that from the additivity of ##S## and the...
  21. Z

    Could Excited Baryon decay into omega meson and baryon?

    Excited baryon could decay into photon and ground state baryon,but could it decay into omega meson and ground state baryon?Could you introduce me some articles about it,experimental or theoretical?
  22. F

    Using v= omega cross r to find instantaneous velocity

    Homework Statement An object is rotating at 4 rad/s about an axis in direction of (2 \hat{i} - 4 \hat{j} + 3\hat{k} ) which then passes through a point (1,2,0)m . Calculate the instantaneous velocity at the point (2,0,3)m (Hint: use \vec{v} = \vec{\omega} \times \vec{r} )Homework Equations...
  23. A

    Couldn't the universe be finite if Omega =1?

    I am not a physicist or a cosmologist, just a science layman who has been doing a lot of reading and thinking. I have been reading a lot in popular literature that if Omega =1, then the universe must also be infinite. Do you think this is just an over-generalization intended for the general...
  24. W

    Sigma Algebra on Omega (Sample Space)

    Respected Members, Suppose Ω is the set of eight possible outcomes of three coin tosses i.e. Ω={{HHH, HHT, HTH, HTTT, THH, THT, TTH, TTT} So if we are not told the results then the sigma algebra ( denoted by F_α) at position α=0 is F_0 = {∅, Ω} Now if are told the first coin toss only...
  25. A

    Spring - Pulley - Mass system. Proving omega is a certain value

    Homework Statement Hello, everyone. I am a starting physics student. I know a little bit of calculus and mechanics. I have been solving a lot of problems successfully, but I come back to being stuck on this one. I will show you what I have done and I hope you can be kind enough to give me a...
  26. K

    What is the variable theta of omega in a series RL cct?

    What is the variable "theta of omega" in a series RL cct? Homework Statement Hi I'm not looking for a complete solution to this problem. My question concerns just one specific part of the solution to part A: why is tan θ(ω) = ωL/R? and what θ(ω) represent? how does it relate to the...
  27. L

    Finding Omega and Zeta from a Magnitude and Phase Plot

    Homework Statement I've been asked to estimate ωn and ζ from the magnitude and phase plot of an atomic force microscope. The magnitude and phase plot is attached. Does anyone know how to solve for these values?
  28. E

    What is the Constant Angular Velocity of a Watch's Second Hand?

    omega of the second hand?? Consider a second hand in the watch. What is the constqant angular velocity. Logicaly, i would say it travels through 1 rev in 1 min so, it is 2∏/60 However, if we look it on the other way, it has angular acceleration so theta= (w node + w final)/2 * t gives 2∏/30...
  29. A

    Omega effect: turning poloidal magnetic field into toroidal field

    Could someone please explain exactly how the omega effect works? It is supposed to explain how a poloidal magnetic field (of the sun for example, or a black hole accretion disk) becomes toroidal. This is supposed to be due to differential rotation and the inertia of mass. But I just don't see...
  30. T

    Omega being less than one in a flat Universe?

    Hi everyone! I'm not very good at math as I'm in high school, and so probably did something wrong in this, but I did some calculations and am now wondering if a flat Universe requires Ω0 ≠ 1? I started with the Friedmann equation, If you divide by 3 and take the inverse of both sides, you...
  31. D

    Big O, Theta & Omega Confusion

    I am getting a little confused over the notations of Big O, Theta, and Omega. I am completely fine with the formal definitions. This is what is confusing me. A problem P has worst case time complexity O(f(n)) and Omega(g(n)). Does this mean that P has worst case time complexity Theta(h(n))...
  32. M

    Polar Kinematics - omega vs. theta_dot?

    Are ω and \dot{θ} the same in a polar kinematics? I know ω is angular speed (rad/s) and it seems to me that \dot{θ} would be the same, but in the context of rotation in polar coordinates where v = \dot{r}\widehat{r}+ r\dot{θ}\widehat{θ}, v = rω, and vθ = r\dot{θ}, that doesn't seem to be...
  33. G

    Solve Laplace Transform for y'' + w^2y = cos(t), y(0) = 1, y'(0) = 0

    Homework Statement y'' + w^2y = cos(t) y(0) = 1 y'(0) = 0 w^2 not equal to 4 Homework Equations Laplace integral, transform via table/memory... Y(s) = F(s) or whatever you like to use The Attempt at a Solution s^2Y(s) - sy(0) - y'(0) + w^2Y(s) = s/(s^2 + 1). Right side is...
  34. B

    Work out B0', E0', k' and omega', and show that the phase (kr-omega t) is

    Homework Statement An electromagnetic planewave with frequency ω is propagating in the x direction in a reference frame S; it is polarised in the y direction with amplitude E_{0}. The k-\omega 4-vector can be written (k_{x}, k_{y}, k_{z}, i\omega/c). a) Write down and define the fields of...
  35. D

    Calculating omega as a function of time for a flywheel

    hiya all, I've done a experiment which was hanging a mass from a light string wrapped around the axis of a flywheel. The mass was released and the flywheel began to rotate. during calculations I've found out it would be great to have ω as a function of time and I've been stuck about how to...
  36. E

    Bijective map of omega tuples

    Homework Statement Find a bijective map : χωxχω\rightarrowχω Homework Equations An omega tuple is a function x:N\rightarrowχ, where χ is a set. χω is the set of all omega tuples of elements of χ. A bijective function is both injective and surjective. The Attempt at a...
  37. E

    Cartesian product of omega tuples

    Homework Statement So I am just trying to understand the concepts here. My main question is what exactly is the cartesian product of an omega tuple? Homework Equations Given a set X, we define an ω-tuple of elements of X to be a function x:N\rightarrowX We denote x as Let...
  38. B

    Spinning Mass and Finding Omega

    Homework Statement http://imageshack.us/f/41/physicsc.png/ My professor gave the following hints: Write down what you know about how r (position of mass from hole) varies with time. Then write Newton's 2nd law in polar coordinates. For part (a), the differential equation that you are looking...
  39. B

    Finding Omega: Evaluating sin^(-1)(3) on the Complex Plane

    Homework Statement if z= sin (omega) find an expression for omega as a function of z that can be used to evaluate all possible values of sin^(-1) (3). Plot these values on the complex plane The Attempt at a Solution z= sin (omega) 3= sin (omega) I don't know how to proceed from...
  40. J

    How does inflation drive omega close to 1?

    Hi I have a question, how does inflation drive omega close to 1? I heard Alan Guth say that inflation drives omega close to 1, how is that so? I hope I can get an answer for this question, I've been looking for it for quite a while.
  41. M

    Proving f(z)=e^(g(z)) on a Convex Set Omega

    Homework Statement Suppose that f is analytic on a convex set omega and that f never vanishes on omega. Prove that f(z)=e^(g(z)) for some analytic function g defined on omega. Hint: does f'/f have a primitive on omega? Homework Equations f(z)=\sum_{k=0}^\infty a_k(z-p)^k The...
  42. D

    When is an expression Big O, Big Omega or Theta?

    I understand how to compare 2 functions and tell which bound they are in... but what I cannot comprehend is, given a single function... how do you write which bound it is in? Given a simple for loop like : for(int i = 0; i<n; i++) { for(int i = 0; i<j; i++) { System.out.println("Haha.")...
  43. S

    Simple harmonic motion (finding omega)

    Homework Statement A particle executes simple harmonic motion with an amplitude of 2.51cm. At what positive displacement from the midpoint of its motion does its speed equal one half of its max speed? Homework Equations A=2.51 cm x(t) = Acos(wt) v(t) = -Awsin(wt) vmax = |-Aw| The...
  44. J

    Understanding Velocity=r(omega)??

    Homework Statement I do not understand why velocity is equal to the radius times the angular velocity. Angular velocity is given in radians per second. How does this equal velocity when multiplied by the radius? Thanks yall! I'm new here by the way. Homework Equations v=r(omega)...
  45. N

    Constructing u(t * omega) from U(t, omega)

    Hello--- I am reading a paper on numerical methods which requires a 2D function to be converted to a 1D function. Let U(t, omega) be the discrete Gabor transform of a sampled signal, where t is time (seconds) and omega is the angular frequency. U(t, omega) is stored in a 2D m-by-n matrix...
  46. C

    Omega Point Theory: Plausible or Pseudoscience?

    Is the omega point theory by Frank J. Tipler plausible? or is it more of a pseudoscientific theory?
  47. Y

    OMEGA Formula: Integrating to Find the Answer

    I guess people who know can help. I know that the final formula should look like this: (OMEGA) = 4tan^(-1) [(e)/n(1+e^2+n^2)^(0.5)] , where e=W/L, n=2z/L I started with D(omega) = dAcos(theta) p^2 cos (theta) = z/p then i did a bunch of...
  48. J

    Uncovering the Truth About Omega 3: Common Questions Answered

    I hope I have chosen the proper forum for this question, if not please accept my apologies and move to the appropiate place. Now for my question. I have recently started to take a little flaxseed oil to up my omega 3 intake, and have noticed that it tastes very fishy. My question is since...
  49. H

    Torque acting on Satellite, why isn't omega increasing?

    Torque acting on Satellite, why isn't omega increasing? Hey guys, HW help problem here, we have a satellite rotating at some constant angular rate, and we are asked to calculate the torque required to maintain said motion. I am able to do this, given the principal Moments of Inertia for the...
  50. E

    Finding Acceleration in Uniform Circular Motion

    circluar motion, "omega" hi, I erased the default format by accident, but it's just a quick question: i and j are unit vectors, w= omega dtheta/dt , theta= angle dependent on time when we have i(-rwsin(theta)) and j(rwcos(theta)) as our velocity vector components, and we wish to find the...
Back
Top