What is meant by Newton's Rules, if A+B=C, A=C and B=C?

  • Context: Undergrad 
  • Thread starter Thread starter PLAGUE
  • Start date Start date
Click For Summary

Discussion Overview

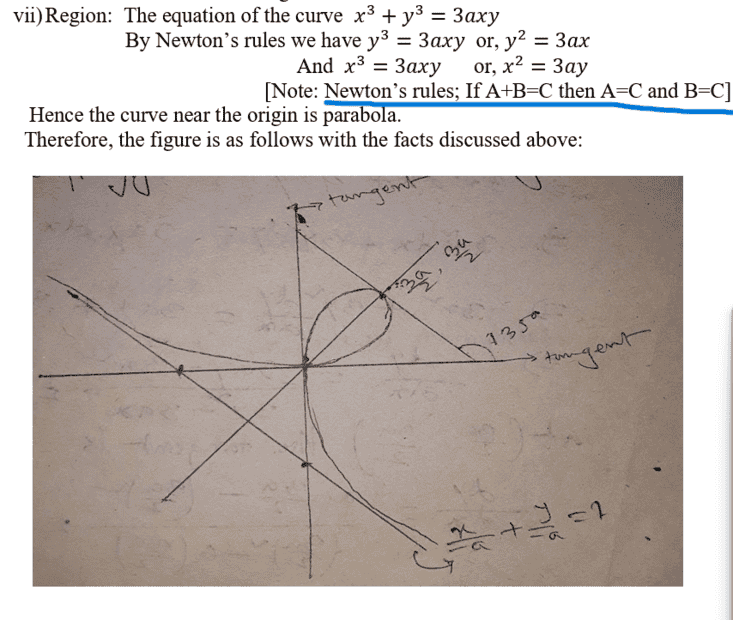
The discussion revolves around the interpretation of "Newton's Rules," particularly in the context of an equation involving multiple variables, A, B, and C. Participants explore the implications of the equation A+B=C, A=C, and B=C, and how it relates to graphing algebraic curves, especially near the origin.

Discussion Character

  • Exploratory
  • Technical explanation
  • Conceptual clarification
  • Debate/contested

Main Points Raised

  • Some participants express uncertainty about the term "Newton's Rules," noting it is not widely recognized or defined in current literature.
  • One participant suggests that the discussion may relate to analyzing behavior near the origin of a graph, particularly when variables are unequal.
  • Another participant introduces an asymptotic principle, proposing that if A(x) + B(x) = C(x) and both tend to infinity, one term should become negligible, indicating a potential relationship between A, B, and C.
  • There is a request for the original problem statement to provide better context for the discussion.
  • One participant mentions that the technique may involve determining the shape of an algebraic curve both close to and far from the origin.

Areas of Agreement / Disagreement

Participants generally do not agree on the definition or implications of "Newton's Rules," and multiple competing views regarding its interpretation and application remain unresolved.

Contextual Notes

Limitations include the lack of clarity on what "Newton's Rules" specifically refers to, as well as the dependence on the original problem statement for full context. The discussion also highlights the complexity of the relationship between A, B, and C, which is not fully explored.

PLAGUE
Messages
37
Reaction score
2
TL;DR
Newton's Rules: if A+B=C, A=C and B=C?
What is it meant by Newton's Rules in point (vii)?
Screenshot 2024-02-21 141024.png
Screenshot 2024-02-21 141049.png
 
Mathematics news on Phys.org
Have you looked up "newton's rules" in the index of the text where you found the problem? Certainly google has turned up nothing relevant, which suggests that it is not a currently or widely used term.

Fronthe context, I guess it has something to do with multiple branches at the origin.
 
Last edited:
I have never heard of this term and couldn't Google it either. I meditated on the technique and I suspect the point is if you're near the origin and x is not equal to y, one of them is smaller, and you can throw out the highest order term in that variable to see locally what the graph looks like. This A+B=C statement is hiding a lot of work if that's what is going on.
 
Reply
  • Like
Likes   Reactions: WWGD and PeroK
There's an asymptotic principle that if ##A(x) + B(x) = C(x)## and both sides tend to infinity, then one of the terms ##A(x)## or ##B(x)## should become negligible towards the limit. So, either ##A(x)## or ##B(x)## is asymptotic to ##C(x)##, but probably not both. That is, of course, only a practical rule of thumb.
 
Reply
  • Informative
  • Like
Likes   Reactions: Gavran and jack action
PLAGUE said:
TL;DR Summary: Newton's Rules: if A+B=C, A=C and B=C?

What is it meant by Newton's Rules in point (vii)?
View attachment 340639View attachment 340641
Maybe you can paste in a copy of the problem statement and not just the conclusion?
 
WWGD said:
Maybe you can paste in a copy of the problem statement and not just the conclusion?
I think the problem statement is draw a graph of ##x^3+y^3=3axy## but I agree it would have been nice
 
Reply
  • Like
Likes   Reactions: WWGD

Similar threads

MHB Find a,b,c,d for Max $a+b-c+d$
  • · Replies 1 ·
Replies
1
Views
1K
MHB Determine all possible values a/(a+b+d)+b/(a+b+c)+c/(b+c+d)+d/(a+c+d)
  • · Replies 2 ·
Replies
2
Views
2K
MHB Find A,B,C for Factorial Equation
  • · Replies 4 ·
Replies
4
Views
2K
MHB Find Product: $(a^4+b^4+c^4)$ and $(a^6+b^6+c^6)$
  • · Replies 3 ·
Replies
3
Views
1K
MHB What is the value of $(a+c)(b+c)(a-d)(b-d)$ given specific roots?
  • · Replies 6 ·
Replies
6
Views
1K
MHB Solve for $d-b$: $a^5=b^4,\,c^3=d^2,\,c-a=19$
  • · Replies 1 ·
Replies
1
Views
1K
High School What is the difference between the two sine rules for resultant vector?
  • · Replies 4 ·
Replies
4
Views
2K
MHB Prove $\sqrt{a}+\sqrt{b}+\sqrt{c}+\sqrt{d}\le 10$ w/ $a,b,c,d>0$
  • · Replies 5 ·
Replies
5
Views
2K
MHB Solving for $(a,\,b,\,c)$ with Powers of 2
  • · Replies 1 ·
Replies
1
Views
1K
MHB What is the value of (a+b)^3+(b+c)^3+(c+a)^3 for the roots of 8x^3+1001x+2008=0?
  • · Replies 2 ·
Replies
2
Views
1K