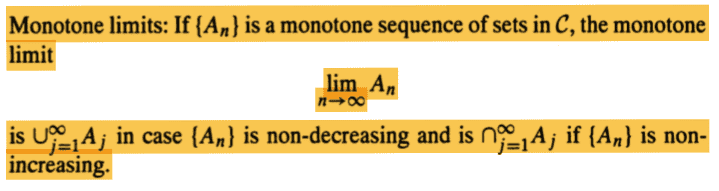
What is the concept of monotone limits?

[jdou86]

TL;DR

Hi all I would like to understand this concept please help.

Summary: Hi all I would like to understand this concept please help.

I understand the montonic convergence theorem this is from a probability theory book and I am confused on understanding it. Please help me understand it.

Thank you very much,Jon.

 

[fresh_42]

You leave a bit of guesswork here: what is $\mathcal{C}$, is the assumed order given by inclusion, and what is the purpose of these limits?

Anyway, the most likely interpretation is a definition of the term monotone limit.

Given a non-decreasing flag of subsets $A_1\subseteq A_2 \subseteq \ldots A_n \subseteq \ldots \,$, i.e. the set $A_{n+1}$ which follows $A_n$ is either equal to $A_n$ or properly includes $A_n$, then the union of all is called (defined) the monotone limit of $\{\,A_n\,:\,n\in \mathbb{N}\,\}$.
Notation: $\lim_{n\to \infty}A_n = \bigcup_{n=1}^\infty A_n$

Given a non-increasing flag of subsets $A_1\supseteq A_2 \supseteq \ldots A_n \supseteq \ldots \,$, i.e. the set $A_{n+1}$ which follows $A_n$ is either equal to $A_n$ or properly included in $A_n$, then the intersection of all is called (defined) the monotone limit of $\{\,A_n\,:\,n\in \mathbb{N}\,\}$.
Notation: $\lim_{n\to \infty}A_n = \bigcap_{n=1}^\infty A_n$

I'm not sure what the book actually says, but to call both by the same name can be confusing. In both cases, it is the set at the "end" of the flags, the set which either includes all $A_n$, resp. the set that is included in all $A_n$.

 

[jdou86]

ah than you very much that helpt me understood it, here are some supplimentary info in case you want it. It's a book called a probability path intended for grad students.

Thanks,
Jon

 

[Erland]

I agree. If the book calls both these "THE monotone limit", this is a linguistic error, since there are two of them.

The first one should be called "The monotone increasing limit", and the second "The monotone decreasing limit", or something like that.

 

[jdou86]

I agree. If the book calls both these "THE monotone limit", this is a linguistic error, since there are two of them.

The first one should be called "The monotone increasing limit", and the second "The monotone decreasing limit", or something like that.

thankfully he called it monotone limits