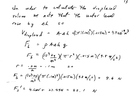TkoT
- 7
- 2
- Homework Statement
- A cylindrical beaker of mass mb = 1.3 kg contains 1.5 x 10^3 ml of water. The beaker is placed on a scale and then a rock of mass mr = 2.2 kg, suspended by a massless string, is totally immersed in the water. The water level rises by 1.5 cm. The diameter of the beaker is 0.2m
a) What mass does the scale measure before the rock is lowered into the water?
b) What mass does the scale measure after the rock is lowered into the water?
- Relevant Equations
- F=mg
my solution:
a)
F(upward)=Fb +Fw
=(1.3+1.5)X9.8
=27.44N
total Mass = 2.8kg
b)
Volume increased = π(0.2/2)^2 x 1.5/100
=4.7x10-4 m^3
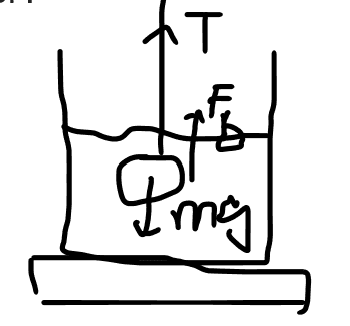
T+Fb =mg
T=mg-Fb
T=2.2x9.8 -1000 x 4.7x10-4 x 9.8
T=17.4N
T is the apparent weight of the rock, so the mass of the rock in the water is 1.74kg
So, the total mass measured by the scale = 1.74 +2.8 = 4.54kg
Question:
I am confused about the part b after I checked the answer. For me, I think the tension represents the apparent weight of the rock. So apparent mass of the rock can be obtained by the tension. But, In the answer, buoyant force is considered as the extra weight added to the scale. That confuses me and I don’t understand why.
answer attached below
a)
F(upward)=Fb +Fw
=(1.3+1.5)X9.8
=27.44N
total Mass = 2.8kg
b)
Volume increased = π(0.2/2)^2 x 1.5/100
=4.7x10-4 m^3
T+Fb =mg
T=mg-Fb
T=2.2x9.8 -1000 x 4.7x10-4 x 9.8
T=17.4N
T is the apparent weight of the rock, so the mass of the rock in the water is 1.74kg
So, the total mass measured by the scale = 1.74 +2.8 = 4.54kg
Question:
I am confused about the part b after I checked the answer. For me, I think the tension represents the apparent weight of the rock. So apparent mass of the rock can be obtained by the tension. But, In the answer, buoyant force is considered as the extra weight added to the scale. That confuses me and I don’t understand why.
answer attached below
Attachments
Last edited: