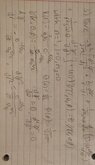Danielk010
- 35
- 4
- Homework Statement
- Show by direct substitution that the wave function corresponding to n = 1, l = 0, m l = 0 is a
solution of Eq. 7.10 corresponding to the ground-state energy of hydrogen.
- Relevant Equations
- Schrodinger's Spherical equation: ## \frac {-\hbar^2} {2m} (\frac {d^2 \psi} {dr^2} + \frac {2} {r} * \frac {d\psi} {dr} + \frac {1} {r^2\sin(\theta)} * \frac {d} {d\theta} * \sin(\theta) *\frac {d\psi} {d\theta} + \frac {1} {r^2\sin(\theta)^2} * \frac {d^2\psi} {d\phi^2}) + U(r) * \psi (r, \theta, \phi) = E * \psi (r, \theta, \phi) ##
Radial equation: ##\frac {2*e^{\frac {-r} {a_0}}} {a_0^{\frac {3} {2}}} ##
Theta equation: ## \frac {1} {\sqrt 2} ##
Phi equation: ## \frac {1} {\sqrt {2\pi}} ##
Wave function = Radial equation * Theta equation * Phi equation
Wave function: ##\frac {e^{\frac {-r} {a_0}}} {\sqrt \pi * a_0^{\frac {3} {2}}} ##
My final energy result: ## \frac {2\pi\varepsilon_0 (-\hbar^2 * r + 2a_0^2\hbar^2) - ma_0^4e^2} {4\pi\varepsilon_0 r a_0^4 m} ##
I attempted the problem by first finding the radial, theta, and phi equation for the ground state of a hydrogen atom. I multiplied the three equations to get the wave equation. From there, I took each derivative in the Schrödinger Spherical equation and found that ## \frac {\partial^2 \psi} {\partial \phi^2} = 0 ## and ## \frac {\partial \psi} {\partial \theta} = 0 ##. From there I found that ## \frac {\partial \psi} {\partial r} = \frac {-e^{\frac {-r} {a_0}}} {\sqrt \pi * a_0^{\frac {5} {2}}} ## and ## \frac {\partial \psi^2} {\partial r^2} = \frac {e^{\frac {-r} {a_0}}} {\sqrt \pi * a_0^{\frac {7} {2}}} ##. I then just plugged in the different equations including, ## U(r) = \frac {-e^2} {4\pi\varepsilon_0 r} ## into the equation to get my final result for energy. Compared to ## E_1 = \frac {-me^4} {32\pi^2\varepsilon_0^2\hbar^2} ## I am not sure if I did the math wrong to not get that energy equation or is there a different energy equation I should use. Thank you for any help provided.