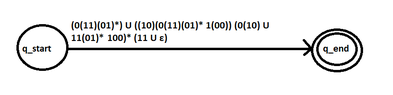evinda
Gold Member
MHB
- 3,741
- 0
Hello! (Wave)
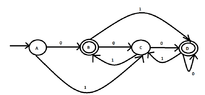
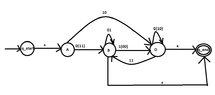
I want to write the language of the automaton with the following transition function in regular form with $A$ as an initial state and $B,D$ as final states.
$$\delta:\begin{matrix}
& & 0 & 1\\
& A & B & C\\
& B & C & D\\
& C & D & B\\
& D & D & C
\end{matrix}$$
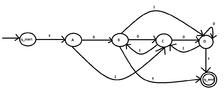
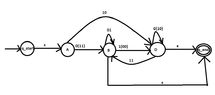
I have drawn the following dfa:
View attachment 5848
Some of the words that the automaton recognizes are the following:
$$0,11,10,000,01,010^{\star},0000^{\star}, 111, 101110$$
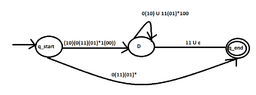
How can we find the general form of the words of the language? (Thinking)
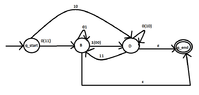
I want to write the language of the automaton with the following transition function in regular form with $A$ as an initial state and $B,D$ as final states.
$$\delta:\begin{matrix}
& & 0 & 1\\
& A & B & C\\
& B & C & D\\
& C & D & B\\
& D & D & C
\end{matrix}$$
I have drawn the following dfa:
View attachment 5848
Some of the words that the automaton recognizes are the following:
$$0,11,10,000,01,010^{\star},0000^{\star}, 111, 101110$$
How can we find the general form of the words of the language? (Thinking)