SUMMARY
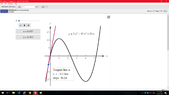
The discussion focuses on determining the inequality form for the slope of the curve defined by the polynomial function \(y=2x^3-15x^2+24x\). The second derivative, calculated as \(y''=12x-30\), indicates where the slope is decreasing. The inequality \(2x-5<0\) leads to the conclusion that the slope is decreasing for \(x < \frac{5}{2}\). This analysis distinguishes between a decreasing slope and a decreasing function, emphasizing the importance of the second derivative in this context.
PREREQUISITES
- Understanding of polynomial functions and their derivatives
- Knowledge of the power rule for differentiation
- Familiarity with the concepts of increasing and decreasing functions
- Basic skills in solving inequalities
NEXT STEPS
- Study the implications of the second derivative test in calculus
- Learn how to analyze polynomial functions for critical points
- Explore the relationship between first and second derivatives in function behavior
- Investigate applications of inequalities in calculus
USEFUL FOR
Students of calculus, mathematics educators, and anyone interested in understanding the behavior of polynomial functions and their derivatives.