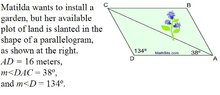
Discussion Overview
The discussion revolves around finding the measure of angle
Discussion Character
- Technical explanation, Mathematical reasoning, Debate/contested, Homework-related
Main Points Raised
- One participant suggests calculating
- Another participant confirms the calculation of 8 degrees is correct, as the angles sum to 180 degrees, and proposes using the Law of Sines for further calculations.
- Several participants provide numerical answers for the lengths AC and AB, and the area of the garden, with one participant questioning the last area calculation and requesting units for clarity.
- Another participant suggests using the cosine law to find AC and provides a formula involving the sine of angle 134 for calculating the area of triangle CDA.
- There is a suggestion to use the formula A = ab sin(θ) for area calculation, with a recommendation to use true values instead of rounded values for accuracy.
Areas of Agreement / Disagreement
Participants generally agree on the calculation of angle
Contextual Notes
Some calculations depend on the accuracy of the values used, and there are unresolved issues regarding the correct height value in the area formula. The discussion does not resolve the area calculation dispute.