What is the Measure of Angle GHD in a Complex Pentagon Configuration?

[anemone]

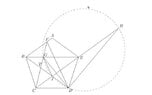
Let $ABCDE$ be a regular pentagon, and let $F$ be a point on $AB$ with $\angle CDF=55^{\circ}$. Suppose $FC$ and $BE$ meet at $G$, and select $H$ on the extension of $CE$ past $E$ such that $\angle DHE=\angle FDG$. FInd the measure of $\angle GHD$ in degrees.

--------------------
Remember to read the http://www.mathhelpboards.com/showthread.php?772-Problem-of-the-Week-%28POTW%29-Procedure-and-Guidelines to find out how to http://www.mathhelpboards.com/forms.php?do=form&fid=2!

 

[anemone]

Re: Problem of the week #107 -April 14th, 2014

No one submitted a solution to this problem. Here is a solution that uses purely geometrical means:

Spoiler

View attachment 2360

Let $J$ be the intersection of diagonals $BD$ and $CE$, and note that $ABEJ$ is a rhombus. First, we claim that $JG$ and $DF$ are parallel.

Let $CF$ and $BD$ meet at $T$. Observe that $\angle TCJ=\angle TFB$ and $\angle BTG=\angle CTJ$ and $\angle GBT=\angle FBG=\angle JCD=\angle JDC=36^{\circ}$

Applying the law of Sines gives $\dfrac{TG}{GF}=\dfrac{TJ}{JD}$, proving the claim.

Then $\angle JGD=\angle FDG=\angle EHD=\angle JHD$ and so $J,\,D,\,G,\,H$ are concyclic. Now we may deduce $\angle GHD=180^{\circ}-\angle GJD=\angle JDF=\angle CDF-36^{\circ}=19^{\circ}$