What is the probability the second orange is sour if the first one is sour?

[evinda]

Hello! (Wave)

A farmer $Α$ has oranges, $10 \%$ of which are sour. A farmer $Β$ has oranges, $4\%$ of which are sour. A client chooses per chance ( with propability $\frac{1}{2}$) two oranges.
Which is the probability, if the first orange that he chooses is sour, that the second is also sour?

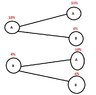
I drawed the following diagram:View attachment 3911Could this help? (Thinking)

 

[I like Serena]

Hi! (Thinking)

That should help, but I think a couple of levels are missing in the decision tree.

I think the first decision the client makes (or rather, the first probability event that occurs) is whether he chooses farmer A or farmer B. (Thinking)
So the root of the tree should have 2 children: A and B, each with probability 1/2.

What do you think the second decision or event is? (Wondering)

 

[soroban]

ello, evinda!

Farmer $Α$ has oranges, 10% of which are sour.
Farmer $Β$ has oranges, 4% of which are sour.
A client chooses a farmer at random, then two of his oranges.
What is the probability, if the first orange is sour,
that the second is also sour?

Bayes' Theorem: $\:P(\text{2nd sour }|\text{1st sour}) \;=\;\dfrac{P(\text{both sour})}{P(\text{1st sour})}$

$P(A) = \frac{1}{2}$
$P(A \wedge \text{1st sour}) = \frac{1}{2}\frac{10}{100}$
$P(A \wedge \text{both sour}) = \frac{1}{2}(\frac{10}{100})^2$

$P(B) = \frac{1}{2}$
$P(B \wedge \text{1st sour}) = \frac{1}{2}\frac{4}{100}$
$P(B \wedge \text{both sour}) = \frac{1}{2}(\frac{4}{100})^2$

$P(\text{both sour}) \:=\: \frac{1}{2}(\frac{10}{100})^2 + \frac{1}{2}(\frac{4}{100})^2 \:=\:\frac{116}{20,000} \:=\:\frac{29}{5000}$

$P(\text{1st sour}) \:=\:\frac{10}{200} + \frac{4}{200} \:=\:\frac{14}{200} \:=\:\frac{7}{100}$

Therefore: $\:P(\text{2nd sour }|\text{ 1st sour}) \;=\; \dfrac{\frac{29}{5000}}{\frac{7}{100}} \;=\;\dfrac{29}{350}$