- #1
mathmari
Gold Member
MHB
- 5,049
- 7
Hey! 
I am looking the following exercise:
If yes, are the justifications correct and complete? Could we improve that or make that more formally?
(Wondering)
I am looking the following exercise:
- At a tango course $12$ married couples participate. Find an appropriate measurable space and calculate the probability that exactly nine couples dance together.
- $5$ women sit at a round table. $3$ men come later. With how many ways can the men sit between the women, if no man can sit next to an other man?
- The measurable space is the tuple $(\Omega, \mathcal{F})$, where $\Omega$ is a set and $\mathcal{F}$ a $\sigma$-Algebra over $\Omega$, right? Is $\Omega$ the set of $12$ men and $12$ women? We have $12$ couples, so $12$ men and $12$ women. We want that $9$ couples dance together.
The first man has the probability $\frac{1}{12}$ to choose the right woman.
The second man has the probability $\frac{1}{11}$ to choose the right woman.
The third man has the probability $\frac{1}{10}$ to choose the right woman.
...
The $i$-th man has the probability $\frac{1}{12-i+1}$ to choose the right woman.
...
The $9$-th man has the probability $\frac{1}{12-9+1}=\frac{1}{4}$ to choose the right woman. The remaining $3$ men have to choose the wrong woman.
The first man has the probability $\frac{2}{3}$ to choose a wrong woman.
The second man has the probability $\frac{1}{2}$ to choose a wrong woman.
The third man has the probability $1$ to choose a wrong woman. So, the probability that exactly nine couples dance together is equal to $$\frac{1}{12}\cdot \frac{1}{11}\cdot \frac{1}{10}\cdot \ldots \cdot \frac{1}{12-i+1}\cdot \ldots \cdot \frac{1}{4}\cdot \frac{2}{3}\cdot \frac{1}{2}\cdot 1$$ - We have the following:
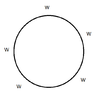
View attachment 7484
right?
The first man has $5$ possibilities to sit between two women.
The second man has $4$ possibilities to sit between two women.
The third man has $3$ possibilities to sit between two women.
Therefore, we get that there are $5\cdot 4\cdot 3$ ways so that the men sit between the women, if no man can sit next to an other man.
If yes, are the justifications correct and complete? Could we improve that or make that more formally?
(Wondering)