internationallove089
- 3
- 0
- TL;DR
- what is multiplication, what is the nature of numbers
As I was thinking about understanding the nature of multiplication and division, understanding the nature of numbers, I thought about the idea that there is something beyond multiplication and repeated addition. Then I thought about dimensional multiplication operations, such as area and volume. I researched the use of number since primitive times. First, let's look at the concept of an apple. Here the apple is a ##3D## object. There may be billions of atoms in one apple. However, we can multiply and collect an apple as we wish. We can perform very good operations in the universe of natural numbers. When we switch to integers, we may encounter some problems. The concept of ##-4## apples is inconsistent.
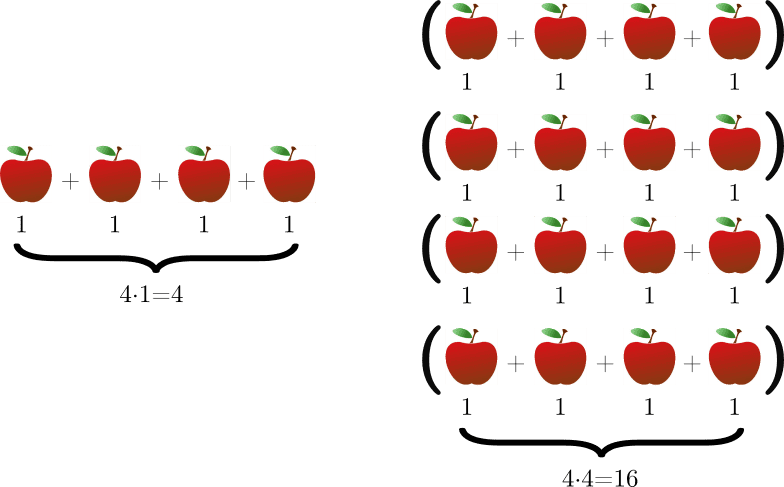
Then I realized that vectors on a one-dimensional number line worked wonderfully to explain operations with integers. However, our numbers here are one-dimensional vectors, not one apple. First of all, our vector ##\overrightarrow{a}## is ##1m## long in the positive direction in the coordinate system. We express this vector with the unit meter. So it is a vector of size 4m. Likewise, if we consider the number as ##4m## in size, independent of direction, the result does not change when multiplying (with positive integers).
$$4\cdot\left| \overrightarrow{a}\right|=4m$$
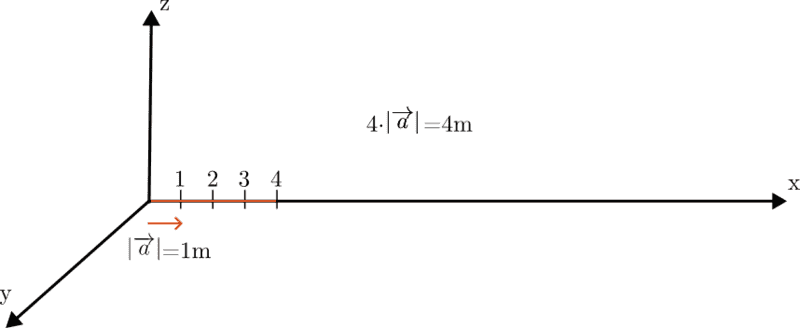
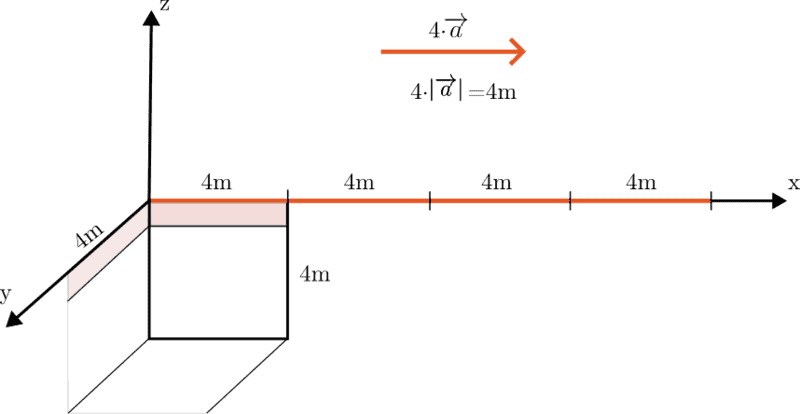
At this point I'm starting to get confused. First of all, when multiplying, dividing, adding and subtracting numbers, we can perform operations between two scalar numbers (apple example). Now let's consider a square with sides ##4m## long. When calculating the perimeter, we are actually performing a multiplication operation on a single dimension. If we multiply one side by ##4##, this means multiplying each unit on the coordinate system by ##4## in one dimension. This Scalar can be the product of two numbers or the product of a vector and a scalar number.
$$4\cdot\left|\overrightarrow{a}\right|\cdot4=4\cdot(0,000000000\overline{1}+0,000000000\overline{1}+.....)=16m$$
Now let's move on to calculating the area. Here we are now working in ##2## dimensions (x and z). Let's have a size that we define as ##4m##. Let's consider it directionally independent. Again, we have an edge defined as 4m in the z direction. Now, while trying to understand the nature of field calculation, I think like this; Multiplying my size of 4m in the x direction by my size in the z direction actually means multiplying my size in the x direction in the z direction for each number value in the z direction. (repeated addition) The interesting thing here is that we are doing the multiplication in two dimensions.
$$4m\cdot4m=4m\cdot(0,000000000\overline{1}+0,000000000\overline{1}+.....)m=16m^{2}$$
When we multiply in ##2## dimensions, the result is like the product of ##2## scalar numbers (apple examples). However, logically, we created the area by adding the length ##x##, ##4m##, infinitely one after the other. Now I have stated my questions below:
- Do numbers have dimensions? Thinking of numbers as one-dimensional vectors works amazingly well when operating with integers. However, is it true that it is in the nature of numbers that we can add them and assign them to different objects, independent of size, as in the apple example (for example, we all intuitively know that the sum of ##1## apple and ##1## apple is ##2##) and that it can have many different natures?
- My other question is, we can multiply a number with the vector whose unit we define on a single dimension. For example ##4m\cdot4## this is quite logical. However, we cannot make ##4m\cdot4m## in one size. But if we think in two dimensions, ##4m\cdot4m=16m^{2}##. Don't we have more 4m sizes than we can count in a ##16m^{2}## area? What's strange is that we can express ##16m## and ##16m^{2}## with the same numbers. This is interesting, don't you think?
Then I realized that vectors on a one-dimensional number line worked wonderfully to explain operations with integers. However, our numbers here are one-dimensional vectors, not one apple. First of all, our vector ##\overrightarrow{a}## is ##1m## long in the positive direction in the coordinate system. We express this vector with the unit meter. So it is a vector of size 4m. Likewise, if we consider the number as ##4m## in size, independent of direction, the result does not change when multiplying (with positive integers).
$$4\cdot\left| \overrightarrow{a}\right|=4m$$
At this point I'm starting to get confused. First of all, when multiplying, dividing, adding and subtracting numbers, we can perform operations between two scalar numbers (apple example). Now let's consider a square with sides ##4m## long. When calculating the perimeter, we are actually performing a multiplication operation on a single dimension. If we multiply one side by ##4##, this means multiplying each unit on the coordinate system by ##4## in one dimension. This Scalar can be the product of two numbers or the product of a vector and a scalar number.
$$4\cdot\left|\overrightarrow{a}\right|\cdot4=4\cdot(0,000000000\overline{1}+0,000000000\overline{1}+.....)=16m$$
Now let's move on to calculating the area. Here we are now working in ##2## dimensions (x and z). Let's have a size that we define as ##4m##. Let's consider it directionally independent. Again, we have an edge defined as 4m in the z direction. Now, while trying to understand the nature of field calculation, I think like this; Multiplying my size of 4m in the x direction by my size in the z direction actually means multiplying my size in the x direction in the z direction for each number value in the z direction. (repeated addition) The interesting thing here is that we are doing the multiplication in two dimensions.
$$4m\cdot4m=4m\cdot(0,000000000\overline{1}+0,000000000\overline{1}+.....)m=16m^{2}$$
When we multiply in ##2## dimensions, the result is like the product of ##2## scalar numbers (apple examples). However, logically, we created the area by adding the length ##x##, ##4m##, infinitely one after the other. Now I have stated my questions below:
- Do numbers have dimensions? Thinking of numbers as one-dimensional vectors works amazingly well when operating with integers. However, is it true that it is in the nature of numbers that we can add them and assign them to different objects, independent of size, as in the apple example (for example, we all intuitively know that the sum of ##1## apple and ##1## apple is ##2##) and that it can have many different natures?
- My other question is, we can multiply a number with the vector whose unit we define on a single dimension. For example ##4m\cdot4## this is quite logical. However, we cannot make ##4m\cdot4m## in one size. But if we think in two dimensions, ##4m\cdot4m=16m^{2}##. Don't we have more 4m sizes than we can count in a ##16m^{2}## area? What's strange is that we can express ##16m## and ##16m^{2}## with the same numbers. This is interesting, don't you think?
Last edited by a moderator: