What is the speed of each particle?

[OierL]

Homework Statement

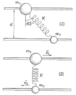
Both m1 and m2 (m1=2m2) masses can slide without friction over parallel and rigid bars that are placed at a distance d from each other. A spring with elastic constant k and with zero natural length connects both masses. The system is placed on a table. The system is released when it is in the state (1) shown in the figure (i.e. when the spring is at 45◦ with the bars). Calculate, when the bodies arrive to state (2) in the figure:

The solution is: v1 =√(k/3m1) ⋅ d

Homework Equations

p=m⋅v
F(spring)=-k⋅x
Ek=1/2⋅m⋅v^2

The Attempt at a Solution

I don't have any idea of how to do this problem... I've been trying to solve it for hours. Please, help!

I have computed that X(enter of mass)=2d/3⋅tan(45º) and that v2=2⋅v1
I don't know how to continue...

 

[gneill]

You need to show what you've tried, even if it didn't work out.

 

[gneill]

Have you at least looked into applicable conservation laws?

 

[haruspex]

I don't have any idea of how to do this problem..

Conservation of work typically doesn't help in finding a time. Think about forces when in some intermediate position.

 

[gneill]

Conservation of work typically doesn't help in finding a time.

I concur and wholeheartedly agree. However, couched beside the figure in the original post is that text: "The solution is: v1 =√(k/3m1) ⋅ d", so it would appear that they are looking for the velocity of m₁ "when" the bodies are positioned as shown in the second figure. The problem is perhaps phrased a tad unfortunately; They are looking for a velocity rather than a time.

 

[haruspex]

I concur and wholeheartedly agree. However, couched beside the figure in the original post is that text: "The solution is: v1 =√(k/3m1) ⋅ d", so it would appear that they are looking for the velocity of m₁ "when" the bodies are positioned as shown in the second figure. The problem is perhaps phrased a tad unfortunately; They are looking for a velocity rather than a time.

Ah yes, the all-important comma. Eats, shoots and leaves.
Unfortunately the images meant to show the whole question are truncated.

Thanks!

 

[gneill]

Ah yes, the all-important comma. Eats, shoots and leaves.

Also agreed. Well said.