What is the voltage across the resistor in this AC circuit problem?

[Ackbach]

Here is this week's University POTW.

-----

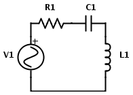
Refer to the following figure:

https://www.physicsforums.com/attachments/3820._xfImport

Given that $R1=1\times 10^6 \, \Omega$, $C1=1\times 10^{-9} \, \text{F}$, and $L1=1\times 10^{-3}\,\text{H}$, and that $V1(t)=120 \cos(120 \pi t)\,\text{V}$, find the voltage across the resistor as a function of time.

-----

Remember to read the http://www.mathhelpboards.com/showthread.php?772-Problem-of-the-Week-%28POTW%29-Procedure-and-Guidelines to find out how to http://www.mathhelpboards.com/forms.php?do=form&fid=2!

 

[Ackbach]

An honorable mention goes to topsquark, who provided some comments about the statement of the problem. I stand by the original problem statement, though. Here is my solution:

Spoiler

Converting to the phasor domain, the voltage is $120\angle 0$, the resistor impedance is $1\text{E6}$, the capacitor impedance is
$$\frac{1}{j\omega C}=\frac{1}{j(120\pi)(1\text{E-9})},$$
and the inductor impedance is $j\omega L=j(120\pi)(1\text{E-3})$. Finding the equivalent impedance involves summing the three impedances. This yields
$$Z_{\text{eq}}=2.835\text{E6} \angle -69.344^{\circ}.$$
Next we find the current phasor by dividing the voltage phasor by the equivalent impedance:
$$I=\frac{V}{Z_{\text{eq}}}=4.233\text{E-5} \angle 69.344^{\circ}.$$
Finally, we may compute the voltage phasor across the resistor by using Ohm's law again:
$$V_{R}=IR=(4.233\text{E-5} \angle 69.344^{\circ})(1\text{E6})
=(4.233\text{E1})\angle 69.344^{\circ}
=42.33 \cos(120\pi t+69.344^{\circ}).$$