What percent of the sky can an astronomer see at one time?

[charlie05]

Homework Statement

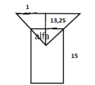
The astronomer fell into the well. The well is circular, depth H = 15m, radius r = 1m. The astronomer has eyes at h = 1.75m. Observation is from the well axis, refraction is neglected.

How many % of sky can an astronomer see at one time?
How many % of sky can an astronomer see during the whole year?

Homework Equations

sine theorem, cosine theorem od sides and angles

The Attempt at a Solution

tg alfa=1/13,25...alfa=0,0013°.
2D well viev...2*alfa=0,0026°

but view is 3D...have I use solid angle? normally an astronomer could see 2π?

 

[CharlieCW]

Since the view is 3D, you should indeed solid angles to calculate the angle of vision. First consider the case were the astronomer is outside the well. In this case, he sees the 100% of the sky (assuming you call 100% seeing the whole half hemisphere on where they're standing). So the solid angle would be $\Omega=2\pi$.

When the astronomer is at the bottom of the well, he is in a cylinder of height 15 m and radius 1 m and his eyes reach up to 1.75 m (assuming he's looking upwards and at the center of the well). Since the differential solid angle is $d\Omega=sin\theta dr d\theta d\phi$, you must integrate within the small region of the well that they can see. The integration on $\phi$ is trivial since it goes from $0$ to $2\pi$, while for $\theta$ you must consider the region they can see from the well.

I cannot draw here, but imagine a triangle rectangle that goes from the eyes of the astronomer to the corners of the well, which has a height of 13.25 m, side of 1 m, and hypothenuse of 13.2877 m. Thus you immediatly see that $sin\theta_w=1/13.2877$ and $\theta_w=arcsin(1/13.2877)$. So your integration goes from $0$ to $\theta_w$. Compare it to $2\pi$ and you get the percentage.

As for how much it will see during the year, you must factor the rotation of the Earth and estimate how much the solid angle will change over time. I haven't worked the math on that one, so I'll leave it to you.

 

[charlie05]

Thank you very much for your help, this is amazing and I understand it...

 

[haruspex]

you must integrate within the small region of the well that they can see

Given the depth to width ratio, probably good enough to consider the area at the top of the well as a flat disc.

 

[CharlieCW]

Given the depth to width ratio, probably good enough to consider the area at the top of the well as a flat disc.

Indeed, in my answer I'm basically considering the top of the well as a flat disk to find an expression for the angle $\theta$.

 

[haruspex]

Indeed, in my answer I'm basically considering the top of the well as a flat disk to find an expression for the angle $\theta$.

That was to find the max θ for your integral. You gave the correct formula for the solid angle, which measures the area of the spherical cap.
I am suggesting just taking the area of the flat disc, no integral needed.