What's wrong with this function

[MHD93]

Hello

What follows is one way of calculating the square root of 2, as Wikipedia shows:

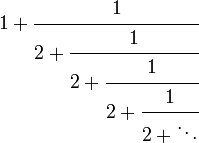
I built the following function as an attempt to express the calculation:

f(x) = 2 + 1 / f(x/2) if x is not 0
f(x) = 1 if x is 0

then square root of 2 = 1 + 1 / f(1)

I used the preceding approach to find the square root of 2, using C++, and it worked..
But the problem is that I have a way for showing that it's wrong!

What's wrong with that function, how can I convince myself logically!?
Thanks for help.. in advance.

 

[mathman]

Something is missing. What is f(x)?

 

[willem2]

Something is missing. What is f(x)?

well, if f(0) = 1. The function relies on floating point rounding to calculate the other values of f(x).

 

[SteveL27]

well, if f(0) = 1. The function relies on floating point rounding to calculate the other values of f(x).

Just curious ... I don't know anything about numerical analysis. To analyze a function like this, do we need to be told the value of N such that 1/N = 0?

 

[JJacquelin]

f(x) = 2 + 1 / f(x/2) if x is not 0
f(x) = 1 if x is 0

This is uncorrect because :
you write (for x=0) f(0) = 1
and f(0) = 2 + 1/f(0)
since f(0)=1 your assuption is 1 = 2 + 1 = 3

 

[disregardthat]

He says "f(x) = 2 + 1 / f(x/2) if x is not 0".

But I still don't see a definition of f(x) when x is not 0.

 

[JJacquelin]

He says "f(x) = 2 + 1 / f(x/2) if x is not 0".

Yes, you are right.

 

[JJacquelin]

I built the following function as an attempt to express the calculation:
f(x) = 2 + 1 / f(x/2) if x is not 0
f(x) = 1 if x is 0

In fact, it isn't the right way.
Let define a function so that g(x)=1/(2+g(x)) any x
So that the infinite fraction is y = 1 + g(x)
What is the function g(x) ?
g(x)=1/(2+g(x))
g(x) (2+g(x)) = 1
(g(x))² + 2g(x) -1 = 0
Solving leads to
g(x) = -1 +(+or-)sqt(1+1)
The positive root is :
g(x) = -1+sqrt(2)
So, the function g(x) is constant.
y = 1 + g(x) = 1 +(-1+sqrt(2))
y = sqrt(2)
The value of the infinite fraction is sqrt(2)

 

[MHD93]

Thanks for replies..

Many said "what is f(x)".. "it's not defined when x isn't 0"..

Actually, I see that it's defined.. here's a similar one:

{
g(x) = g(x/2) if x isn't zero
g(0) = 1
}

Let's try to find g(1)

Well.. by definition: g(1) = g(1/2) = g(1/4) = g(1/8) ...
In the end.. and after infinitely many steps.. doesn't the number between parentheses have to be 0, and then g(1) = g(0) = 1

??

That's the method I'm thinking about.. is it right?

 

[agentredlum]

Thanks for replies..

Many said "what is f(x)".. "it's not defined when x isn't 0"..

Actually, I see that it's defined.. here's a similar one:

{
g(x) = g(x/2) if x isn't zero
g(0) = 1
}

Let's try to find g(1)

Well.. by definition: g(1) = g(1/2) = g(1/4) = g(1/8) ...
In the end.. and after infinitely many steps.. doesn't the number between parentheses have to be 0, and then g(1) = g(0) = 1

??

That's the method I'm thinking about.. is it right?

I think that is pretty clever. You used your BRAIN to come up with a logical definition for f(0).

 

[SteveL27]

Thanks for replies..

Many said "what is f(x)".. "it's not defined when x isn't 0"..

Actually, I see that it's defined.. here's a similar one:

{
g(x) = g(x/2) if x isn't zero
g(0) = 1
}

Let's try to find g(1)

Well.. by definition: g(1) = g(1/2) = g(1/4) = g(1/8) ...
In the end.. and after infinitely many steps.. doesn't the number between parentheses have to be 0, and then g(1) = g(0) = 1

??

That's the method I'm thinking about.. is it right?

No, it's not right. Your function is not well-defined for any nonzero value. That's why the only way it makes sense is in the context of numerical analysis, when on some particular hardware, 1/N = 0 for sufficiently large N.

If your domain is the real numbers and you are using ordinary real number arithmetic, then how are you going to compute f(1)? You would have to do infinitely many operations and take a limit. That's not a valid definition of a function.

In a real world, physical computer, at some point 1/N is zero. That's numerical analysis ... when you take into account the physical representation of numbers in a computer.

 

[disregardthat]

Well.. by definition: g(1) = g(1/2) = g(1/4) = g(1/8) ...
In the end.. and after infinitely many steps.. doesn't the number between parentheses have to be 0, and then g(1) = g(0) = 1

??

That's the method I'm thinking about.. is it right?

That method requires that g is continuous. An extra assumption.

 

[agentredlum]

If your method reproduces the continued fraction expansion of sqrt(2) then i don't see anything wrong with using it.

I used your iterative function to reproduce the continued fraction expansion of sqrt(2) by hand, on paper.

If you are going to focus on technicalities why it shouldn't work then you are in danger of disregarding the fact that it DOES work.

It's sort of like grounding a plane because one of the passenger seats is missing...