- 2,180
- 2,721
Here is the function that I have written:
and here is how I call the function:
Here is the graph that I get:
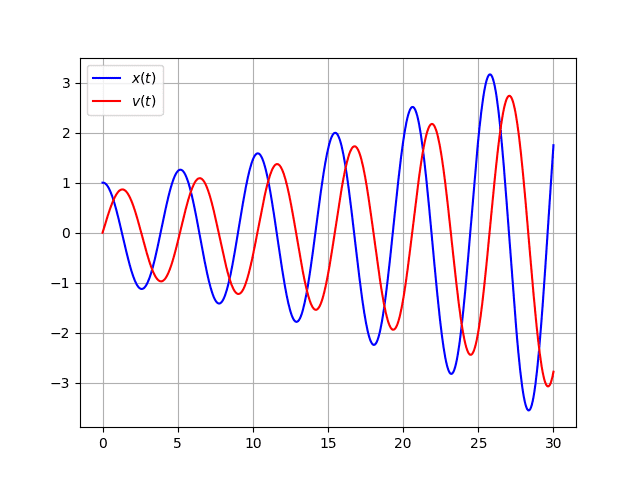
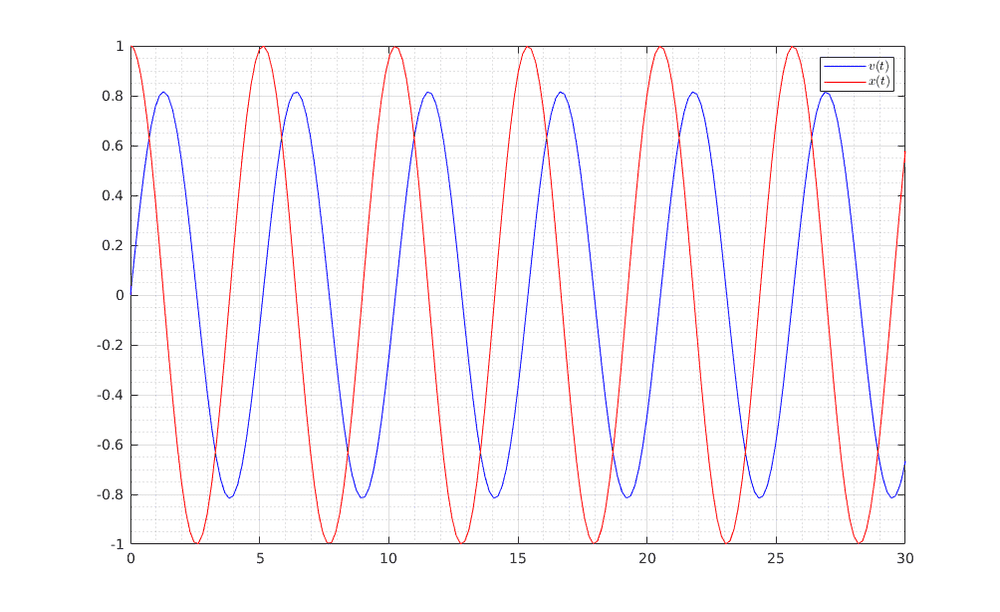
If I run the (almost) same program in MATLAB using
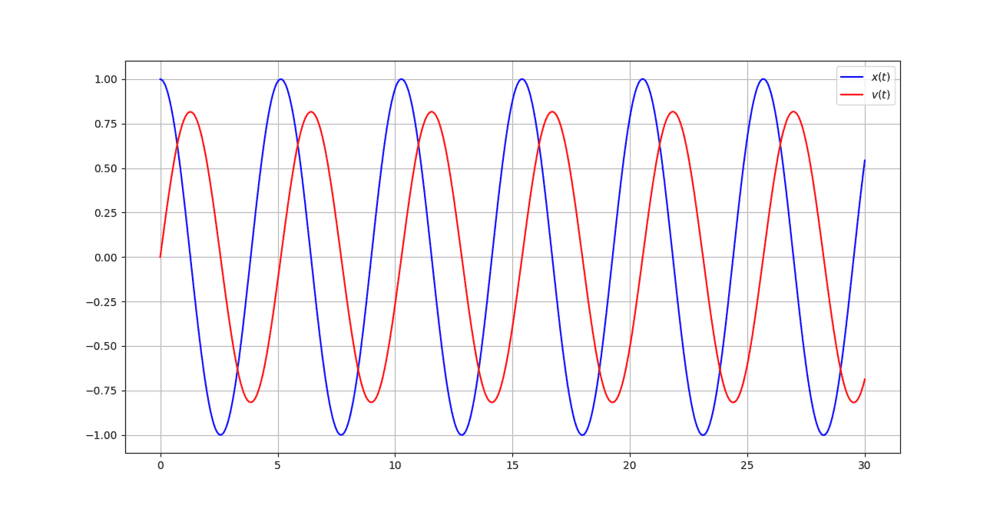
In Python, I have also written functions for RK2 midpoint, Heun's and Ralston's algorithms. If I solve the problem using the first one of those functions, I get the following graph:
This matches the plot from MATLAB, which means there is something wrong with the Euler's algorithm function that I have written. Can anyone please point out the error?
Python:
import numpy as np
def ode_euler_forward(odefun, y_initial, x_range, num_steps):
"""
Solves a system of non-stiff ODEs using Euler's forward algorithm.
Parameters
----------
odefun : callable(x, y1, y2, ...)
The function that represents the system of ODEs.
y_initial : tuple
The initial values of all the dependent variables in the form (y_1_initial, y_2_initial, ...)
If there is only one variable, turn it into a tuple with a trailing comma: (y_initial,)
x_range : tuple
The start and the end values of the independent variable in the form (x_start, x_end)
num_steps : int
The number of steps to be used.
Returns
-------
x, y : tuple
The values of the independent variable, and corresponding values of each dependent variable in the form
(np.ndarray, np.ndarray).
"""
x_initial = x_range[0]
x_end = x_range[1]
h = (x_end - x_initial) / num_steps # The size of each step
y_initial = np.asarray(y_initial)[np.newaxis, :]
# y = [[y_initial], [0, 0, ...], [0, 0, ...], ...]. Each row will hold the value from one iteration.
y = np.vstack((y_initial, np.zeros((num_steps - 1, np.size(y_initial, 1)), dtype=float)))
x = np.linspace(x_initial, x_end, num_steps)[np.newaxis, :].T
for i in range(0, num_steps - 1):
y[i + 1, :] = y[i, :] + h * odefun(x[i], y[i, :][np.newaxis, :])
return x, y
Python:
import numpy as np
import matplotlib.pyplot as plt
m = 10
k = 15
def myODE(t, x): return np.array([x[0, 1], -k * x[0, 0] / m])[np.newaxis, :]
tSol, xSol_euler = ode_euler_forward(myODE, (0.0, 1.0), (0.0, 30.0), 501)
plt.plot(tSol, xSol_euler[:, 1], '-b', label=r'$x(t)$')
plt.plot(tSol, xSol_euler[:, 0], '-r', label=r'$v(t)$')
plt.legend(loc='best')
plt.grid(True, which='both')
plt.show()If I run the (almost) same program in MATLAB using
ode45, here is the graph I get:In Python, I have also written functions for RK2 midpoint, Heun's and Ralston's algorithms. If I solve the problem using the first one of those functions, I get the following graph:
This matches the plot from MATLAB, which means there is something wrong with the Euler's algorithm function that I have written. Can anyone please point out the error?
Last edited: