When is a Twice Continuously Differentiable Function Locally Convex?

[baiyang11]

Convex function and convex set(#1 edited)

Please answer #4, where I put my questions more specific. Thank you very much!

The question is about convex function and convex set. Considering a constrained nonlinear programming (NLP) problem
\[min \quad f({\bf x}) \quad {\bf x}\in \mathbb{R}^{n} \]
\[s.t. \quad g_{i}({\bf x})\leq 0 \quad i=1,2,...,N \]
\[\quad\quad h_{j}({\bf x})=0 \quad j=1,2,...,M \]

Where \(g_{i}({\bf x})\) and \(h_{j}({\bf x})\) is twice continuously differentiable. The feasible region \( S=\{{\bf x}|g_{i}({\bf x}),h_{j}({\bf x}),\forall i,j\}\). It is known that if \(g_{i}({\bf x})\) is convex and \(h_{j}({\bf x})\) is affinely linear for \({\bf x}\in \mathbb{R}^{n}\), \(S\) is a convex set. However, in my problem, \(g_{i}({\bf x})\) and \(h_{j}({\bf x})\) is indefinite for \({\bf x}\in \mathbb{R}^{n}\). So I would like to ask if there is any theory may answer the following two questions:

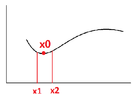
(1)For any twice continuously differentiable but indefinite function \(g_{i}({\bf x})\), on what condition, \(g_{i}({\bf x})\) is convex in a neighborhood of a point \({\bf x_{0}}\in\mathbb{R}^{n}\) ? (A guess is that Hessian of \(g_{i}\) at \({\bf x_{0}}\) is positive semidefinite. Is that the case?)
View attachment 989
Just like the image above. The function is indefinite for all \(x\), but is locally convex in the neighborhood of \(x_{0}\), which is \((x_{1},x_{2})\).

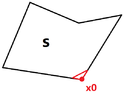
(2)On what condition, a neighborhood in \(S\) of a feasible point \({\bf x_{0}}\in S\) is a convex set? (I suppose a sufficient condition is that every \(g_{i}({\bf x})\) and \(h_{j}({\bf x})\) is convex in a neighborhood of \({\bf x_{0}}\). But is that necessary?)
View attachment 990
Just like the image above. The set \(S\) is not convex, but is locally convex in the neighborhood of \({\bf x_{0}}\) (the red triangle set).

 

[Opalg]

To be convenient, I wrote down my question in a .doc file as attachments. Because the doc file is out of max file size, so I made it .zip file. Please refer to the .zip attachment. Sorry for the inconvenience.
The question is about convex function and convex set.
Thanks very much!

Most people are very wary about opening zip files from unknown sources. If you have a genuine question, I suggest that you ask it in text form.

 

[baiyang11]

Most people are very wary about opening zip files from unknown sources. If you have a genuine question, I suggest that you ask it in text form.

Thank you! I've edited the #1 and ask the question in text form.

 

[baiyang11]

(1) Given a twice continuously differentiable function $$f(x),x\in\mathbb{R}$$, it can be justified that $$f''(x)$$ is not always positive for $$\forall x\in\mathbb{R}$$. However, if $$f''(x_0)>0$$, is $$f(x)$$ ("locally") convex in some epsilon distance around $$x_0$$? (As shown in the 1st picutre in #1)

(2) Given a twice continously differentiable function $$f({\bf x}),{\bf x}\in\mathbb{R}^{n}$$, it can be justified that Hessian Matrix of $$f({\bf x})$$ is not always postive definite for $$\forall x\in\mathbb{R}^{n}$$. However, if Hessian of $$f({\bf x})$$ at $${\bf x_0}$$ is positve definite, is $$f({\bf x})$$ ("locally") convex in some epsilon neighborhood of $${\bf x_0}$$?

(3) Given a region $$S$$ defined by $$g_{i}({\bf x})\leq 0 \quad i=1,2,...,N$$ and $$h_{j}({\bf x})=0 \quad j=1,2,...,M$$ and $${\bf x}\in\mathbb{R}^{n}$$ (usually $$S$$ defines the feasible region of a general constrained optimization problem), where every $$g_{i}({\bf x})$$ and $$h_{j}({\bf x})$$ is twice continously differentiable. Here $$g_{i}({\bf x})$$ is not convex for $$\forall {\bf x}\in\mathbb{R}^{n}$$, $$h_{j}({\bf x})$$ is not affinely linear, so $$S$$ is not a convex set "as a whole". But for a feasible point $${\bf x_0}\in S$$, on what condition (I would like to know condition about $$g_{i}({\bf x})$$ and $$h_{j}({\bf x})$$, not just the "at + (1-t)b" definition of convexity set), a neighborhood of $${\bf x_0}$$ in $$S$$ is ("locally") convex? (As shown in the 2nd picture in #1)
As to this question, if this kind of condition exists, Hessian of $$g_{i}({\bf x_0})$$ and $$h_{j}({\bf x_0})$$ is probably involved, as I guessed.

I believe these three questions make it easier for you to answer exactly. Thanks very much!