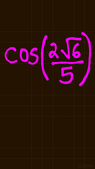Which angle has a larger cosine value?

[mathdad]

We are given the following:

Let B = beta

cos B = cos (2_/6)/5

cos θ = cos 3/4

Which angle is larger:

cos (B - π/2) or cos (θ + π/2)?

I found cos (B - π/2) to be about 0.557.

I found cos (θ + π/2 to be about 0.731.

So, 0.731 > 0.557.

My answer is cos (θ + π/2) > cos (B - π/2).

Book's answer is cos (B - π/2) > cos (θ + π/2).

Why is my answer wrong?

 

[skeeter]

what is this value supposed to be?

(2_/6)/5

 

[mathdad]

what is this value supposed to be?

See picture.

View attachment 7938

 

[skeeter]

recheck the problem ... are you sure it's not

$\cos{\beta} = \dfrac{2\sqrt{6}}{5}$ and $\cos{\theta} = \dfrac{3}{4}$

instead of

$\cos{\beta} = \cos\left(\dfrac{2\sqrt{6}}{5}\right)$ and $\cos{\theta} = \cos\left(\dfrac{3}{4}\right)$

?

 

[mathdad]

Yes, you are right. So, why is the textbook right? Why is my answer wrong?

 

[skeeter]

Yes, you are right. So, why is the textbook right? Why is my answer wrong?

one more note regarding the problem statement ...

Which angle is larger:

cos (B - π/2) or cos (θ + π/2)?

$\cos\left(\beta - \dfrac{\pi}{2}\right)$ and $\cos\left(\theta + \dfrac{\pi}{2}\right)$ are not angle values ... maybe which value of cosine is larger?

one more question, does the problem statement say anything about which quadrant(s) $\beta$ and $\theta$ terminate?

 

[mathdad]

one more note regarding the problem statement ...
$\cos\left(\beta - \dfrac{\pi}{2}\right)$ and $\cos\left(\theta + \dfrac{\pi}{2}\right)$ are not angle values ... maybe which value of cosine is larger?

one more question, does the problem statement say anything about which quadrant(s) $\beta$ and $\theta$ terminate?

I need to get back to you. I will look in the textbook.