Solving trigonometric equations as fractions of π

[AN630078]

Homework Statement:

Trigonometric equations are by far one of my weakest areas. I have been practising to improve and refine my understanding but I am still a little uncertain in areas. I have attempted some questions below but was wondering if anyone could offer me some advice on how to improve my workings or apply more suitable methods.

Question 1; Solve the following equations giving your solutions as exact fractions of π in the range 0 ≤θ ≤2 π:

a. sin θ=√3/2
b.cos2θ=0.5
c.tan (2θ-π/4)=1

Relevant Equations:

π

Question 1;
a. sin θ=√3/2
θ=arcsin √3/2
θ=π/3 rad
sin √3/2=60 degrees
60 degrees *π/180=π/3 rad.

To find the other solutions in the range, sin θ=sin(π-θ)
π-π/3=2π/3
The solutions are π/3 and 2π/3 in the range 0 ≤θ ≤2 π

b. cos2θ=0.5
2θ=arccos 0.5
2θ=π/3 rad
Divide both sides by 2;
θ=π/6 rad

To find the other solutions in the range, cos θ=cos(2π-θ)
2π-π/3=5π/3
Divide by 2 =5π/6

The solutions are π/6 and 5π/6 in the range 0 ≤θ ≤2 π

c. tan (2θ-π/4)=1
2θ-π/4=arctan 1
2θ-π/4 = π/4
Add π/4 to both sides;
2θ=π/4+π/4
2θ=π/2
Divide both sides by 2:
θ=π/4

To find other solutions in the range add π/2:
π/4+π/2=3π/4
3π/4+π/2=5π/4
5π/4+π/2=7π/4

The solutions are π/4, 3π/4, 5π/4 and 7π/4 in the range 0 ≤θ ≤2 π

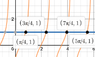
I have also attached what I think the graphs of these equations would look like to find the required solutions. How can I improve or broaden my answers to more extensively exhibit my workings. I am a little confused here admittedly.

 

[BvU]

Question 1; Solve the following equations giving your solutions as exact fractions of π in the range 0 ≤θ ≤2 π:

b.cos2θ=0.5

b. cos2θ=0.5
2θ=arccos 0.5
2θ=π/3 rad
Divide both sides by 2;
θ=π/6 rad

Safer: $$\cos 2\theta = \cos{\pi\over 3} $$
$$2\theta = \pm {\pi\over 3} + 2n\pi $$
$$\theta = \pm {\pi\over 6} + n\pi $$
$$0\le\theta\le2\pi\Rightarrow\quad \theta = {\pi\over 6}, \ {5\pi\over 6}, \ {7\pi\over 6}, \ {11\pi\over 6} $$so you don't miss the last two !
(your picture does show the third one)

 

[epenguin]

Quick look your answers seem okay, not checked them all.

However the way you set them out is in my view not quite logical,Might only just convince a Prof that you had understood.

You write out in each case a trigonometrical function equals something.
Then the next line the same equation in inverse form, i.e. in terms of the inverse (arc) function.
The you say this function has this numerical value, degs or rads.
But why?

I think it would be clearer and more helpful to yourself if you just draw out the two simple standard triangles where particular angles occur, mark the lengths of sides, then the values of the trigonometrical functions of the angles (degs or rads) occur will be obvious, and also the corresponding inverses, given the side' ratios.

Your diagram for getting the multiple values of some solutions is perfectly useful.

The purpose of this exercise this is to instil a certain familiarity – these angles and their values turn up rather often in the math and applications, e.g. Electrical engineering. More often than not over the years whenever a case came up I had to do a little diagram.

 

[AN630078]

Safer: $$\cos 2\theta = \cos{\pi\over 3} $$
$$2\theta = \pm {\pi\over 3} + 2n\pi $$
$$\theta = \pm {\pi\over 6} + n\pi $$
$$0\le\theta\le2\pi\Rightarrow\quad \theta = {\pi\over 6}, \ {5\pi\over 6}, \ {7\pi\over 6}, \ {11\pi\over 6} $$so you don't miss the last two !
(your picture does show the third one)

Thank you for your reply and for exhibing a safer alternative. So similarly trying to mirror your approach say for a;

a. sin θ= sin π/3
θ=arcsin π/3

How could I progress from here?

 

[AN630078]

Quick look your answers seem okay, not checked them all.

However the way you set them out is in my view not quite logical,Might only just convince a Prof that you had understood.

You write out in each case a trigonometrical function equals something.
Then the next line the same equation in inverse form, i.e. in terms of the inverse (arc) function.
The you say this function has this numerical value, degs or rads.
But why?

I think it would be clearer and more helpful to yourself if you just draw out the two simple standard triangles where particular angles occur, mark the lengths of sides, then the values of the trigonometrical functions of the angles (degs or rads) occur will be obvious, and also the corresponding inverses, given the side' ratios.

Your diagram for getting the multiple values of some solutions is perfectly useful.

The purpose of this exercise this is to instil a certain familiarity – these angles and their values turn up rather often in the math and applications, e.g. Electrical engineering. More often than not over the years whenever a case came up I had to do a little diagram.

Thank you for your reply. Yes, I agree it is not logical and I am still rather confused confessedly !

Ok taking your approach;

a. sinθ= sinπ/3
θ= arcsin π/3
θ=π/3 +2πn, θ=2π/3 +2πn

Therefore, in 0 ≤θ ≤2 π, θ=π/3 and θ=2π/3

b. cos2θ=cos π/3
2θ=π/3 +2πn
θ=π/6 +πn

In 0 ≤θ ≤2 π, θ=π/6, 5π/6, 7π/6,11π/6

c. tan (2θ-π/4)=tan π/4
2θ-π/4 = π/4 + πn
θ=π/4 + πn/2

In 0 ≤θ ≤2 π, θ=π/4, 3π/4,5π/4,7π/4

I will draw out two triangles as you have suggested and mark where the angles occur to better familiarise myself as suggested, thank you for the suggestion 😁👍

 

[epenguin]

Thank you for your reply. Yes, I agree it is not logical and I am still rather confused confessedly !

Ok

I will draw out two triangles as you have suggested and mark where the angles occur to better familiarise myself as suggested, thank you for the suggestion 😁👍

Yes, you do that. The way you set it out as though you thought it needed some very formal sounding proof makes you sound intimidated, which you admit you are.

Just draw out these two triangles: an equilateral triangle, and an isosceles right angled triangle, both with a bisector of the angle, write in the angles, it is most convenient to let the length of the longest side of the resulting right angled triangles be 2 and call that side $a$', write on the paper the obvious length of one of the other sides and call it $b$ and then write near the third side "from Pythagoras theorem, $c=..."$, write e.g. $cos α = b/a$ etc. and all the ratios for a all the angles, pin it up on your bedroom wall, leave it there till you're sick of it. That way the near triviality of it it will sink in, then when you need it in an exam you might have forgotten it but write the diagram and it will come back.