Discussion Overview
The discussion revolves around a mechanical mechanism found in an old book, focusing on its kinematic properties, including the path of movement of its links and potential applications. Participants explore mathematical techniques for analyzing the mechanism, particularly in terms of its geometric and kinematic characteristics.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
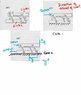
- One participant inquires about mathematical techniques to determine the locus of travel for the mechanism's links, specifically addressing the nonlinear curve of one link.
- Another participant describes the function of the links and suggests potential applications, comparing the mechanism to folding chairs and baby carriages.
- A different participant questions how to find the path of movement for one link when another link is included, proposing that it may involve superposition of movements.
- There is a discussion about the mechanism being classified as over-determined due to the presence of more unknowns than equations, with references to kinematic terms and criteria.
- Participants mention the Kutzbach criterion and Gruebler's criterion in the context of determining degrees of freedom for the mechanism.
- One participant provides a historical context for the mechanism, describing its use as a parallel rule for navigators and discussing its design features.
- Another participant expresses interest in the mathematical implications of the mechanism's design, particularly regarding the linearization of scales used in conjunction with the mechanism.
- There are requests for references to the original book where the mechanism was found, including details about its author and publication year.
Areas of Agreement / Disagreement
Participants express various viewpoints on the mechanism's classification and kinematic properties, with no consensus reached on the exact nature of its movement or applications. Multiple competing views remain regarding the analysis of the mechanism.
Contextual Notes
Participants note the complexity of the mechanism due to the nonlinear curve and the implications of rigid versus non-rigid links, which may affect the analysis of its kinematics. There are unresolved mathematical steps regarding the transformation matrix for the curved link.
Who May Find This Useful
Readers interested in mechanical engineering, kinematics, historical mechanisms, and mathematical modeling of mechanical systems may find this discussion relevant.