brotherbobby
- 756
- 170
- Homework Statement
- Indicate the points on the plane ##xOy## that satisfy the given equation : ##\mathbf{|y|x=x}##
- Relevant Equations
- By definition, the modulus of a number ##|x| = x\; \text{if}\; x \geq 0## and ##|x| = -x\; \text{if}\; x < 0##.
Given the equation : ##|y| x = x##.
Two conditions are possible :
(1) ##\underline{y\geq 0}## : ##xy = x\Rightarrow \boxed{y = 1}\; (x \neq 0)##. We note that except for zero, ##-\infty<x<+\infty## for this case.
(2) ##\underline{y < 0}## : ##-xy = x\Rightarrow \boxed{y = -1}\; (x \neq 0)##. We note that except for zero, ##-\infty<x<+\infty## for this case.
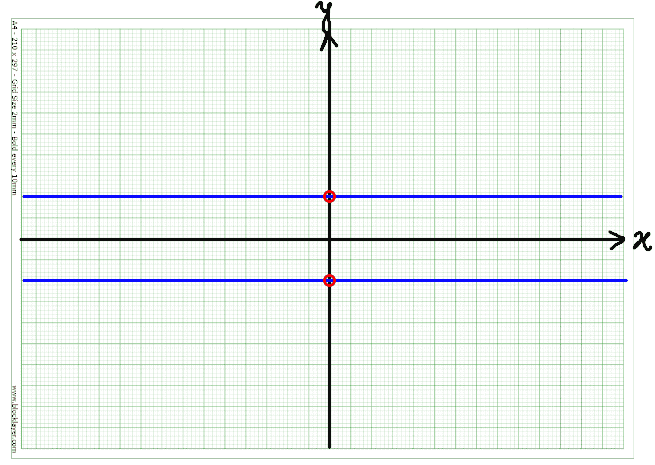 Hence the graph for this equation is (shown to the right) :
Hence the graph for this equation is (shown to the right) :
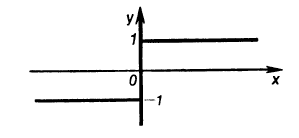 However, it is a different answer as given in the book (shown on the left).
However, it is a different answer as given in the book (shown on the left).
As I have mentioned, ##x \in (-\infty, +\infty)\; \text{but}\; x \neq 0##. Hence I see no reason (for the book) to omit the negative values of ##x## for the solution ##y = 1## and the positive values of ##x## for the solution ##y = -1##.
Where am I going wrong with the reasoning? Or, dare I ask, is the book mistaken?
Two conditions are possible :
(1) ##\underline{y\geq 0}## : ##xy = x\Rightarrow \boxed{y = 1}\; (x \neq 0)##. We note that except for zero, ##-\infty<x<+\infty## for this case.
(2) ##\underline{y < 0}## : ##-xy = x\Rightarrow \boxed{y = -1}\; (x \neq 0)##. We note that except for zero, ##-\infty<x<+\infty## for this case.
As I have mentioned, ##x \in (-\infty, +\infty)\; \text{but}\; x \neq 0##. Hence I see no reason (for the book) to omit the negative values of ##x## for the solution ##y = 1## and the positive values of ##x## for the solution ##y = -1##.
Where am I going wrong with the reasoning? Or, dare I ask, is the book mistaken?